2025年暑假作业完美假期生活八年级数学湖南教育出版社
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年暑假作业完美假期生活八年级数学湖南教育出版社 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
9. 如图,一个平行四边形被分成面积分别为 $ S _ { 1 } $,$ S _ { 2 } $,$ S _ { 3 } $,$ S _ { 4 } $ 的四个小平行四边形,当 $ C D $ 沿 $ A B $ 自左向右在平行四边形内平行滑动时,则 $ S _ { 1 } S _ { 4 } $ 与 $ S _ { 2 } S _ { 3 } $ 的大小关系为____.
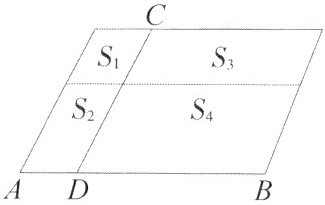
____处填入答案后为:
9. 如图,一个平行四边形被分成面积分别为 $ S _ { 1 } $,$ S _ { 2 } $,$ S _ { 3 } $,$ S _ { 4 } $ 的四个小平行四边形,当 $ C D $ 沿 $ A B $ 自左向右在平行四边形内平行滑动时,则 $ S _ { 1 } S _ { 4 } $ 与 $ S _ { 2 } S _ { 3 } $ 的大小关系为


____处填入答案后为:
9. 如图,一个平行四边形被分成面积分别为 $ S _ { 1 } $,$ S _ { 2 } $,$ S _ { 3 } $,$ S _ { 4 } $ 的四个小平行四边形,当 $ C D $ 沿 $ A B $ 自左向右在平行四边形内平行滑动时,则 $ S _ { 1 } S _ { 4 } $ 与 $ S _ { 2 } S _ { 3 } $ 的大小关系为
$ S _ { 1 } S _ { 4 } = S _ { 2 } S _ { 3 } $
.
答案:
$ S _ { 1 } S _ { 4 } = S _ { 2 } S _ { 3 } $
10. 如图,平行四边形 $ A B C D $ 的对角线 $ A C $ 的垂直平分线与边 $ A D $,$ B C $ 分别相交于点 $ E $,$ F $.
求证:四边形 $ A F C E $ 是菱形.
证明:
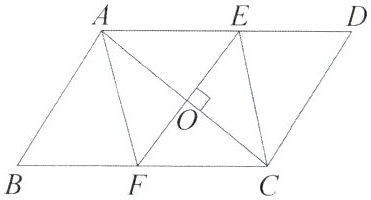
求证:四边形 $ A F C E $ 是菱形.
证明:
∵ 四边形 ABCD 是平行四边形,∴ AD // BC. ∴ $ ∠ E A C = ∠ F C A $. ∵ EF 是 AC 的垂直平分线,∴ OA = OC,$ ∠ E O A = ∠ F O C $,EA = EC. 在 $ △ E O A $ 和 $ △ F O C $ 中,$ ∠ E A O = ∠ F C O $,AO = CO,$ ∠ E O A = ∠ F O C $,∴ $ △ E O A ≌ △ F O C $. ∴ AE = CF. ∴ 四边形 AFCE 是平行四边形. 又 ∵ EA = EC,∴ 四边形 AFCE 是菱形.

答案:
证明:
∵ 四边形 ABCD 是平行四边形,
∴ AD // BC.
∴ $ ∠ E A C = ∠ F C A $.
∵ EF 是 AC 的垂直平分线,
∴ OA = OC,$ ∠ E O A = ∠ F O C $,EA = EC. 在 $ △ E O A $ 和 $ △ F O C $ 中,$ ∠ E A O = ∠ F C O $,AO = CO,$ ∠ E O A = ∠ F O C $,
∴ $ △ E O A ≌ △ F O C $.
∴ AE = CF.
∴ 四边形 AFCE 是平行四边形. 又
∵ EA = EC,
∴ 四边形 AFCE 是菱形.
∵ 四边形 ABCD 是平行四边形,
∴ AD // BC.
∴ $ ∠ E A C = ∠ F C A $.
∵ EF 是 AC 的垂直平分线,
∴ OA = OC,$ ∠ E O A = ∠ F O C $,EA = EC. 在 $ △ E O A $ 和 $ △ F O C $ 中,$ ∠ E A O = ∠ F C O $,AO = CO,$ ∠ E O A = ∠ F O C $,
∴ $ △ E O A ≌ △ F O C $.
∴ AE = CF.
∴ 四边形 AFCE 是平行四边形. 又
∵ EA = EC,
∴ 四边形 AFCE 是菱形.
11. 如图,在平行四边形 $ A B C D $ 中,若 $ A B = 6 $,$ A D = 10 $,$ \angle A B C $ 的平分线交 $ A D $ 于点 $ E $,交 $ C D $ 的延长线于点 $ F $,求 $ D F $ 的长为
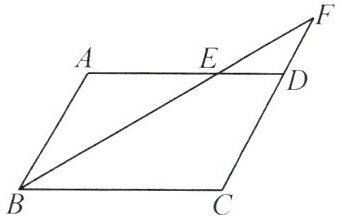
4
。
答案:
4
12. 如图,在四边形 $ A B C D $ 中,$ \angle A B C = 90 ^ { \circ } $,$ A C = A D $,$ M $,$ N $ 分别为 $ A C $,$ C D $ 的中点,连接 $ B M $,$ M N $,$ B N $。
(1)求证:$ B M = M N $;
(2)若 $ \angle B A D = 60 ^ { \circ } $,$ A C $ 平分 $ \angle B A D $,$ A C = 2 $,求 $ B N $ 的长。
(1)
(2)
(1)求证:$ B M = M N $;
(2)若 $ \angle B A D = 60 ^ { \circ } $,$ A C $ 平分 $ \angle B A D $,$ A C = 2 $,求 $ B N $ 的长。
(1)
略
(2)
$ \sqrt { 2 } $
答案:
(1) 略
(2) $ \sqrt { 2 } $
(1) 略
(2) $ \sqrt { 2 } $
13. 如图,在矩形 $ A B C D $ 中,$ A B = 5 $,$ A D = 3 $,点 $ P $ 是 $ A B $ 边上一点(不与 $ A $,$ B $ 重合),连接 $ C P $,过点 $ P $ 作 $ P Q \perp C P $ 交 $ A D $ 边于点 $ Q $,连接 $ C Q $. 当 $ \triangle C D Q \cong \triangle C P Q $ 时,求 $ A Q $ 的长为
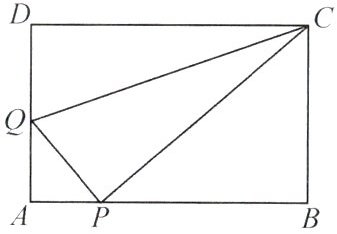
$ \frac { 4 } { 3 } $
.
答案:
$ \frac { 4 } { 3 } $
查看更多完整答案,请扫码查看


