2025年暑假作业完美假期生活八年级数学湖南教育出版社
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年暑假作业完美假期生活八年级数学湖南教育出版社 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 下列命题中,真命题是(
A. 四边相等的四边形是正方形
B. 对角线相等的菱形是正方形
C. 正方形的两条对角线相等,但不互相垂直平分
D. 矩形、菱形、正方形都具有“对角线相等”的性质
B
)A. 四边相等的四边形是正方形
B. 对角线相等的菱形是正方形
C. 正方形的两条对角线相等,但不互相垂直平分
D. 矩形、菱形、正方形都具有“对角线相等”的性质
答案:
B
2. 如图,正方形 $ABCD$ 中,$AB = 3$,点 $E$ 在边 $CD$ 上,且 $CD = 3DE$。将 $\triangle ADE$ 沿 $AE$ 对折至 $\triangle AFE$,延长 $EF$ 交边 $BC$ 于点 $G$,连接 $AG$,$CF$。有下列结论:①点 $G$ 是 $BC$ 中点;②$FG = FC$;③$S_{\triangle RGC}=\frac{9}{10}$。其中正确的是(
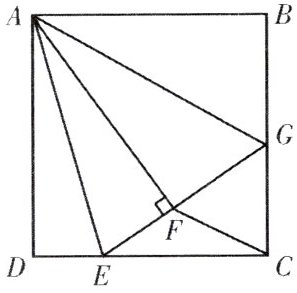
A. ①②
B. ①③
C. ②③
D. ①②③
B
)
A. ①②
B. ①③
C. ②③
D. ①②③
答案:
B
3. 如图,在菱形 $ABCD$ 中,$\angle BAD = 120^{\circ}$。已知 $\triangle ABC$ 的周长是 15,则菱形 $ABCD$ 的周长是(
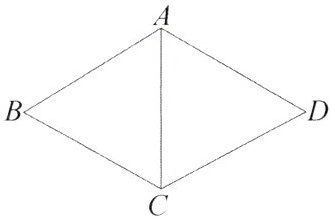
A. 25
B. 20
C. 15
D. 10
B
)
A. 25
B. 20
C. 15
D. 10
答案:
B
4. 如图,$DE$ 是 $\triangle ABC$ 的中位线,过点 $C$ 作 $CF// BD$ 交 $DE$ 的延长线于点 $F$,则下列结论正确的是(
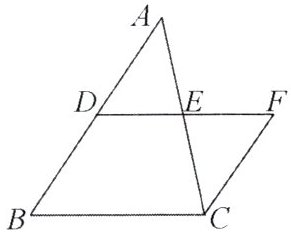
A. $EF = CF$
B. $EF = DE$
C. $CF < BD$
D. $EF > DE$
B
)
A. $EF = CF$
B. $EF = DE$
C. $CF < BD$
D. $EF > DE$
答案:
B
5. 如图,矩形 $ABCD$ 的两条对角线相交于点 $O$,$\angle AOD = 60^{\circ}$,$AD = 2$,则 $AC$ 的长是(
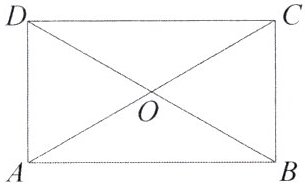
A. 2
B. 4
C. $2\sqrt{3}$
D. $4\sqrt{3}$
B
)
A. 2
B. 4
C. $2\sqrt{3}$
D. $4\sqrt{3}$
答案:
B
6. 四边形 $ABCD$ 中,对角线 $AC$,$BD$ 相交于点 $O$,给出下列四个条件:
① $AD// BC$;② $AD = BC$;③ $OA = OC$;④ $OB = OD$。
从中任选两个条件,能使四边形 $ABCD$ 为平行四边形的选法有(
A. 3 种
B. 4 种
C. 5 种
D. 6 种
① $AD// BC$;② $AD = BC$;③ $OA = OC$;④ $OB = OD$。
从中任选两个条件,能使四边形 $ABCD$ 为平行四边形的选法有(
B
)A. 3 种
B. 4 种
C. 5 种
D. 6 种
答案:
B
查看更多完整答案,请扫码查看


