《2025年暑假作业完美假期生活八年级数学湖南教育出版社》

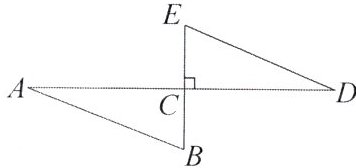
11. 如图，点$C$为$AD$的中点，过点$C$的线段$BE\perp AD$，且$AB = DE$.求证：$AB// ED$.
证明：因为点$C$为$AD$的中点，所以$AC = DC$。
又因为$BE\perp AD$，所以$\angle ACB=\angle DCE = 90^{\circ}$。
在$Rt\triangle ACB$和$Rt\triangle DCE$中，$\left\{\begin{array}{l}AB = DE\\AC = DC\end{array}\right.$，$\therefore Rt\triangle ACB\cong Rt\triangle DCE(HL)$，$\therefore\angle A=\angle D$，$\therefore AB// ED$。

答案： 【解析】：
因为点$C$为$AD$的中点，所以$AC = DC$。
又因为$BE\perp AD$，所以$\angle ACB=\angle DCE = 90^{\circ}$。
在$Rt\triangle ACB$和$Rt\triangle DCE$中，$\left\{\begin{array}{l}AB = DE\\AC = DC\end{array}\right.$，根据$HL$（斜边 - 直角边）定理，可得$Rt\triangle ACB\cong Rt\triangle DCE$。
由全等三角形的性质可知$\angle A=\angle D$。
根据内错角相等，两直线平行，所以$AB// ED$。
【答案】：
在$Rt\triangle ACB$和$Rt\triangle DCE$中，$\left\{\begin{array}{l}AB = DE\\AC = DC\end{array}\right.$，$\therefore Rt\triangle ACB\cong Rt\triangle DCE(HL)$，$\therefore\angle A=\angle D$，$\therefore AB// ED$。

12. 已知：一次函数$y = kx + b$的图象经过$M(0,2)$，$N(1,3)$两点.
（1）求$k$，$b$的值；$k$的值为$1$，$b$的值为$2$
（2）若一次函数$y = kx + b$的图象与$x$轴的交点为$A(a,0)$，$a$的值为$-2$

答案：
(1) $ k = 1 $，$ b = 2 $
(2) $ a = - 2 $

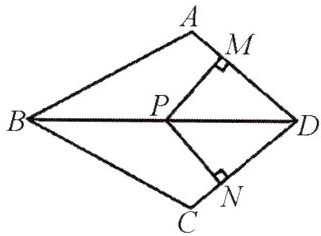
13. 如图，在四边形$ABCD$中，$AB = BC$，对角线$BD$平分$\angle ABC$，$P$是$BD$上一点，过点$P$作$PM\perp AD$，$PN\perp CD$，垂足分别为点$M$，$N$.
（1）求证：$\angle ADB=\angle CDB$；
（2）若$\angle ADC = 90^{\circ}$，求证：四边形$MPND$是正方形.

答案： 【解析】：
### $(1)$ 证明$\angle ADB = \angle CDB$
已知$BD$平分$\angle ABC$，根据角平分线的定义可得$\angle ABD=\angle CBD$。
在$\triangle ABD$和$\triangle CBD$中，$\begin{cases}AB = BC\\\angle ABD=\angle CBD\\BD = BD\end{cases}$（公共边）。
根据全等三角形判定定理中的“边角边”（$SAS$），可以得出$\triangle ABD\cong\triangle CBD$。
再根据全等三角形的性质，全等三角形的对应角相等，所以$\angle ADB=\angle CDB$。
### $(2)$ 证明四边形$MPND$是正方形
已知$PM\perp AD$，$PN\perp CD$，所以$\angle PMD=\angle PND = 90^{\circ}$。
又因为$\angle ADC = 90^{\circ}$，根据“有三个角是直角的四边形是矩形”，可得四边形$MPND$是矩形。
由$(1)$知$\angle ADB=\angle CDB$，$PM\perp AD$，$PN\perp CD$，根据“角平分线上的点到角两边的距离相等”，可得$PM = PN$。
再根据“一组邻边相等的矩形是正方形”，所以四边形$MPND$是正方形。
【答案】：
$(1)$ 证明见上述解析；$(2)$ 证明见上述解析。