2025年快乐假期暑假作业延边教育出版社五年级数学北师大版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年快乐假期暑假作业延边教育出版社五年级数学北师大版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 直接写出得数。
$\frac {3}{5}+\frac {2}{5}=$
$\frac {10}{11}-\frac {1}{3}=$
$\frac {8}{15}×\frac {3}{8}=$
$\frac {3}{5}+\frac {2}{5}=$
1
$9÷\frac {3}{4}=$12
$\frac {3}{8}×2=$$\frac{3}{4}$
$\frac {3}{4}÷\frac {1}{4}=$3
$\frac {10}{11}-\frac {1}{3}=$
$\frac{19}{33}$
$\frac {5}{12}×\frac {4}{5}=$$\frac{1}{3}$
$\frac {5}{9}×\frac {5}{9}=$$\frac{25}{81}$
$\frac {7}{11}×\frac {1}{11}=$$\frac{7}{121}$
$\frac {8}{15}×\frac {3}{8}=$
$\frac{1}{5}$
$1-\frac {4}{23}=$$\frac{19}{23}$
$\frac {4}{5}×6=$$\frac{24}{5}$
$\frac {7}{9}+\frac {2}{3}=$$\frac{13}{9}$
答案:
【解析】:
1. 同分母分数相加,分母不变,分子相加,$\frac{3}{5}+\frac{2}{5}=\frac{3 + 2}{5}=1$;
2. 一个数除以分数等于这个数乘分数的倒数,$9\div\frac{3}{4}=9\times\frac{4}{3}=12$;
3. 分数乘整数,用分数的分子和整数相乘的积做分子,分母不变,$\frac{3}{8}\times2=\frac{3\times2}{8}=\frac{3}{4}$;
4. 一个数除以分数等于这个数乘分数的倒数,$\frac{3}{4}\div\frac{1}{4}=\frac{3}{4}\times4 = 3$;
5. 异分母分数相减,先通分,$\frac{10}{11}-\frac{1}{3}=\frac{30}{33}-\frac{11}{33}=\frac{30 - 11}{33}=\frac{19}{33}$;
6. 分数乘分数,用分子相乘的积做分子,分母相乘的积做分母,$\frac{5}{12}\times\frac{4}{5}=\frac{5\times4}{12\times5}=\frac{1}{3}$;
7. 分数乘分数,$\frac{5}{9}\times\frac{5}{9}=\frac{5\times5}{9\times9}=\frac{25}{81}$;
8. 分数乘分数,$\frac{7}{11}\times\frac{1}{11}=\frac{7\times1}{11\times11}=\frac{7}{121}$;
9. 分数乘分数,$\frac{8}{15}\times\frac{3}{8}=\frac{8\times3}{15\times8}=\frac{1}{5}$;
10. 把$1$化为$\frac{23}{23}$,$1-\frac{4}{23}=\frac{23}{23}-\frac{4}{23}=\frac{23 - 4}{23}=\frac{19}{23}$;
11. 分数乘整数,$\frac{4}{5}\times6=\frac{4\times6}{5}=\frac{24}{5}$;
12. 先通分,$\frac{7}{9}+\frac{2}{3}=\frac{7}{9}+\frac{6}{9}=\frac{7 + 6}{9}=\frac{13}{9}$。
【答案】:$1$ $12$ $\frac{3}{4}$ $3$ $\frac{19}{33}$ $\frac{1}{3}$ $\frac{25}{81}$ $\frac{7}{121}$ $\frac{1}{5}$ $\frac{19}{23}$ $\frac{24}{5}$ $\frac{13}{9}$
1. 同分母分数相加,分母不变,分子相加,$\frac{3}{5}+\frac{2}{5}=\frac{3 + 2}{5}=1$;
2. 一个数除以分数等于这个数乘分数的倒数,$9\div\frac{3}{4}=9\times\frac{4}{3}=12$;
3. 分数乘整数,用分数的分子和整数相乘的积做分子,分母不变,$\frac{3}{8}\times2=\frac{3\times2}{8}=\frac{3}{4}$;
4. 一个数除以分数等于这个数乘分数的倒数,$\frac{3}{4}\div\frac{1}{4}=\frac{3}{4}\times4 = 3$;
5. 异分母分数相减,先通分,$\frac{10}{11}-\frac{1}{3}=\frac{30}{33}-\frac{11}{33}=\frac{30 - 11}{33}=\frac{19}{33}$;
6. 分数乘分数,用分子相乘的积做分子,分母相乘的积做分母,$\frac{5}{12}\times\frac{4}{5}=\frac{5\times4}{12\times5}=\frac{1}{3}$;
7. 分数乘分数,$\frac{5}{9}\times\frac{5}{9}=\frac{5\times5}{9\times9}=\frac{25}{81}$;
8. 分数乘分数,$\frac{7}{11}\times\frac{1}{11}=\frac{7\times1}{11\times11}=\frac{7}{121}$;
9. 分数乘分数,$\frac{8}{15}\times\frac{3}{8}=\frac{8\times3}{15\times8}=\frac{1}{5}$;
10. 把$1$化为$\frac{23}{23}$,$1-\frac{4}{23}=\frac{23}{23}-\frac{4}{23}=\frac{23 - 4}{23}=\frac{19}{23}$;
11. 分数乘整数,$\frac{4}{5}\times6=\frac{4\times6}{5}=\frac{24}{5}$;
12. 先通分,$\frac{7}{9}+\frac{2}{3}=\frac{7}{9}+\frac{6}{9}=\frac{7 + 6}{9}=\frac{13}{9}$。
【答案】:$1$ $12$ $\frac{3}{4}$ $3$ $\frac{19}{33}$ $\frac{1}{3}$ $\frac{25}{81}$ $\frac{7}{121}$ $\frac{1}{5}$ $\frac{19}{23}$ $\frac{24}{5}$ $\frac{13}{9}$
2. 解方程。
$x-\frac {1}{3}x=\frac {5}{6}$
$x+\frac {1}{5}x=3.6$
$x-\frac {2}{5}x=\frac {7}{20}×4$
$x+\frac {1}{3}x=12$
$x-\frac {2}{5}x=\frac {27}{100}$
$\frac {3}{10}x=63$
$x-\frac {1}{3}x=\frac {5}{6}$
$\frac{5}{4}$
$x+\frac {1}{5}x=3.6$
3
$x-\frac {2}{5}x=\frac {7}{20}×4$
$\frac{7}{3}$
$x+\frac {1}{3}x=12$
9
$x-\frac {2}{5}x=\frac {27}{100}$
$\frac{9}{20}$
$\frac {3}{10}x=63$
210
答案:
【解析】:
1. 对于方程$x - \frac{1}{3}x=\frac{5}{6}$,先合并同类项得$\frac{2}{3}x=\frac{5}{6}$,再根据等式的性质,两边同时除以$\frac{2}{3}$,即$x=\frac{5}{6}\div\frac{2}{3}=\frac{5}{6}\times\frac{3}{2}=\frac{5}{4}$。
2. 对于方程$x+\frac{1}{5}x = 3.6$,合并同类项得$\frac{6}{5}x = 3.6$,将$3.6$化为分数$\frac{18}{5}$,则$x=\frac{18}{5}\div\frac{6}{5}=\frac{18}{5}\times\frac{5}{6}=3$。
3. 对于方程$x-\frac{2}{5}x=\frac{7}{20}\times4$,先计算右边$\frac{7}{20}\times4=\frac{7}{5}$,再合并左边同类项得$\frac{3}{5}x=\frac{7}{5}$,两边同时除以$\frac{3}{5}$,$x=\frac{7}{5}\div\frac{3}{5}=\frac{7}{5}\times\frac{5}{3}=\frac{7}{3}$。
4. 对于方程$x+\frac{1}{3}x = 12$,合并同类项得$\frac{4}{3}x = 12$,两边同时除以$\frac{4}{3}$,$x=12\div\frac{4}{3}=12\times\frac{3}{4}=9$。
5. 对于方程$x-\frac{2}{5}x=\frac{27}{100}$,合并同类项得$\frac{3}{5}x=\frac{27}{100}$,两边同时除以$\frac{3}{5}$,$x=\frac{27}{100}\div\frac{3}{5}=\frac{27}{100}\times\frac{5}{3}=\frac{9}{20}$。
6. 对于方程$\frac{3}{10}x = 63$,两边同时除以$\frac{3}{10}$,$x=63\div\frac{3}{10}=63\times\frac{10}{3}=210$。
【答案】:1.$\frac{5}{4}$ 2. $3$ 3. $\frac{7}{3}$ 4. $9$ 5. $\frac{9}{20}$ 6. $210$
1. 对于方程$x - \frac{1}{3}x=\frac{5}{6}$,先合并同类项得$\frac{2}{3}x=\frac{5}{6}$,再根据等式的性质,两边同时除以$\frac{2}{3}$,即$x=\frac{5}{6}\div\frac{2}{3}=\frac{5}{6}\times\frac{3}{2}=\frac{5}{4}$。
2. 对于方程$x+\frac{1}{5}x = 3.6$,合并同类项得$\frac{6}{5}x = 3.6$,将$3.6$化为分数$\frac{18}{5}$,则$x=\frac{18}{5}\div\frac{6}{5}=\frac{18}{5}\times\frac{5}{6}=3$。
3. 对于方程$x-\frac{2}{5}x=\frac{7}{20}\times4$,先计算右边$\frac{7}{20}\times4=\frac{7}{5}$,再合并左边同类项得$\frac{3}{5}x=\frac{7}{5}$,两边同时除以$\frac{3}{5}$,$x=\frac{7}{5}\div\frac{3}{5}=\frac{7}{5}\times\frac{5}{3}=\frac{7}{3}$。
4. 对于方程$x+\frac{1}{3}x = 12$,合并同类项得$\frac{4}{3}x = 12$,两边同时除以$\frac{4}{3}$,$x=12\div\frac{4}{3}=12\times\frac{3}{4}=9$。
5. 对于方程$x-\frac{2}{5}x=\frac{27}{100}$,合并同类项得$\frac{3}{5}x=\frac{27}{100}$,两边同时除以$\frac{3}{5}$,$x=\frac{27}{100}\div\frac{3}{5}=\frac{27}{100}\times\frac{5}{3}=\frac{9}{20}$。
6. 对于方程$\frac{3}{10}x = 63$,两边同时除以$\frac{3}{10}$,$x=63\div\frac{3}{10}=63\times\frac{10}{3}=210$。
【答案】:1.$\frac{5}{4}$ 2. $3$ 3. $\frac{7}{3}$ 4. $9$ 5. $\frac{9}{20}$ 6. $210$
1. 北偏西$30^{\circ }$,还可以说成(
A. 南偏西$30^{\circ }$
B. 西偏北$30^{\circ }$
C. 西偏北$60^{\circ }$
C
)。A. 南偏西$30^{\circ }$
B. 西偏北$30^{\circ }$
C. 西偏北$60^{\circ }$
答案:
C
2. 如图,小强看小林在(
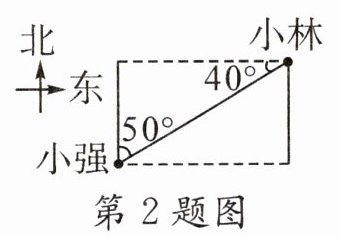
A. 北偏东$50^{\circ }$
B. 东偏北$50^{\circ }$
C. 西偏南$40^{\circ }$
A
)方向上,小林看小强在(C
)方向上。
A. 北偏东$50^{\circ }$
B. 东偏北$50^{\circ }$
C. 西偏南$40^{\circ }$
答案:
A、C
3.
(1)以超市为观测点,商场在(
A. 正南方 B. 正西方 C. 正东方
(2)以超市为观测点,学校在(
A. 东偏南$30^{\circ }$ B. 南偏东$30^{\circ }$ C. 西偏北$30^{\circ }$
(3)从绿苑小区出发,走(
A. 4 B. 5 C. 6
(1)以超市为观测点,商场在(
B
)。A. 正南方 B. 正西方 C. 正东方
(2)以超市为观测点,学校在(
A
)方向上。A. 东偏南$30^{\circ }$ B. 南偏东$30^{\circ }$ C. 西偏北$30^{\circ }$
(3)从绿苑小区出发,走(
B
)站就到学校了。A. 4 B. 5 C. 6
答案:
1. B 2. A 3. B
查看更多完整答案,请扫码查看


