《2025年快乐假期暑假作业延边教育出版社五年级数学北师大版》

1. 口算。
$\frac {5}{6}÷\frac {5}{12}=$2 $\frac {7}{16}×8=$$\frac{7}{2}$ $9÷\frac {1}{10}=$90 $\frac {2}{3}×\frac {9}{10}=$$\frac{3}{5}$
$\frac {3}{5}×\frac {1}{3}=$$\frac{1}{5}$ $\frac {5}{18}×\frac {9}{20}=$$\frac{1}{8}$ $63×\frac {2}{9}=$14 $12÷\frac {4}{5}=$15
$1÷\frac {1}{8}=$8 $74×\frac {5}{37}=$10 $2÷\frac {2}{7}=$7 $\frac {2}{5}+\frac {1}{3}=$$\frac{11}{15}$

答案： 【解析】：
1. 对于$\frac{5}{6}\div\frac{5}{12}$，根据分数除法法则，除以一个分数等于乘以它的倒数，即$\frac{5}{6}\times\frac{12}{5} = 2$。
2. 对于$\frac{7}{16}\times8$，整数与分数相乘，整数与分子相乘作分子，分母不变，$\frac{7\times8}{16}=\frac{7}{2}$。
3. 对于$9\div\frac{1}{10}$，根据分数除法法则，$9\times10 = 90$。
4. 对于$\frac{2}{3}\times\frac{9}{10}$，分子相乘作分子，分母相乘作分母，再约分，$\frac{2\times9}{3\times10}=\frac{3}{5}$。
5. 对于$\frac{3}{5}\times\frac{1}{3}$，分子相乘作分子，分母相乘作分母，$\frac{3\times1}{5\times3}=\frac{1}{5}$。
6. 对于$\frac{5}{18}\times\frac{9}{20}$，分子相乘作分子，分母相乘作分母，再约分，$\frac{5\times9}{18\times20}=\frac{1}{8}$。
7. 对于$63\times\frac{2}{9}$，整数与分数相乘，$63$与$9$约分后计算，$7\times2 = 14$。
8. 对于$12\div\frac{4}{5}$，根据分数除法法则，$12\times\frac{5}{4}=15$。
9. 对于$1\div\frac{1}{8}$，根据分数除法法则，$1\times8 = 8$。
10. 对于$74\times\frac{5}{37}$，$74$与$37$约分后计算，$2\times5 = 10$。
11. 对于$2\div\frac{2}{7}$，根据分数除法法则，$2\times\frac{7}{2}=7$。
12. 对于$\frac{2}{5}+\frac{1}{3}$，先通分，$\frac{2\times3}{5\times3}+\frac{1\times5}{3\times5}=\frac{6}{15}+\frac{5}{15}=\frac{11}{15}$。
【答案】：$2$ $\frac{7}{2}$ $90$ $\frac{3}{5}$ $\frac{1}{5}$ $\frac{1}{8}$ $14$ $15$ $8$ $10$ $7$ $\frac{11}{15}$

2. 解方程。
$6x-\frac {1}{2}=0.5$ $x = \frac{1}{6}$ $\frac {7}{10}x+5=96$ $x = 130$ $\frac {1}{2}x+\frac {2}{3}x=21$ $x = 18$
$x+\frac {1}{4}x=100$ $x = 80$ $x-\frac {1}{9}x=16$ $x = 18$ $\frac {3}{5}+\frac {1}{2}x=0.9$ $x = 0.6$

答案： 【解析】：
1. 对于方程$6x - \frac{1}{2} = 0.5$，先将$0.5$化为$\frac{1}{2}$，则方程变为$6x-\frac{1}{2}=\frac{1}{2}$，两边同时加$\frac{1}{2}$得$6x=\frac{1}{2}+\frac{1}{2}=1$，两边再同时除以$6$，解得$x = \frac{1}{6}$。
2. 对于方程$\frac{7}{10}x + 5 = 96$，两边同时减$5$得$\frac{7}{10}x=96 - 5 = 91$，两边再同时除以$\frac{7}{10}$，即$x = 91\div\frac{7}{10}=91\times\frac{10}{7}=130$。
3. 对于方程$\frac{1}{2}x+\frac{2}{3}x = 21$，先通分，$\frac{1}{2}x+\frac{2}{3}x=\frac{3}{6}x+\frac{4}{6}x=\frac{7}{6}x$，则$\frac{7}{6}x = 21$，两边同时除以$\frac{7}{6}$，即$x = 21\div\frac{7}{6}=21\times\frac{6}{7}=18$。
4. 对于方程$x+\frac{1}{4}x = 100$，$x+\frac{1}{4}x=\frac{4}{4}x+\frac{1}{4}x=\frac{5}{4}x$，则$\frac{5}{4}x = 100$，两边同时除以$\frac{5}{4}$，即$x = 100\div\frac{5}{4}=100\times\frac{4}{5}=80$。
5. 对于方程$x-\frac{1}{9}x = 16$，$x-\frac{1}{9}x=\frac{9}{9}x-\frac{1}{9}x=\frac{8}{9}x$，则$\frac{8}{9}x = 16$，两边同时除以$\frac{8}{9}$，即$x = 16\div\frac{8}{9}=16\times\frac{9}{8}=18$。
6. 对于方程$\frac{3}{5}+\frac{1}{2}x = 0.9$，先将$\frac{3}{5}$化为$0.6$，则方程变为$0.6+\frac{1}{2}x = 0.9$，两边同时减$0.6$得$\frac{1}{2}x=0.9 - 0.6 = 0.3$，两边再同时除以$\frac{1}{2}$，即$x = 0.3\div\frac{1}{2}=0.3\times2 = 0.6$。
【答案】：1.$x = \frac{1}{6}$ 2.$x = 130$ 3.$x = 18$ 4.$x = 80$ 5.$x = 18$ 6.$x = 0.6$

3. 用简便方法计算下面各题。
$\frac {4}{5}+\frac {5}{17}+\frac {1}{5}$ $9.625-\frac {16}{9}-\frac {2}{9}$ $\frac {19}{21}-\frac {5}{24}+\frac {2}{21}-\frac {7}{24}$

答案： 【解析】：
1. 对于$\frac{4}{5}+\frac{5}{17}+\frac{1}{5}$，利用加法交换律$a + b + c = a + c + b$，可得$\frac{4}{5}+\frac{1}{5}+\frac{5}{17}$，先计算$\frac{4}{5}+\frac{1}{5}=1$，再计算$1+\frac{5}{17}=1\frac{5}{17}$。
2. 对于$9.625-\frac{16}{9}-\frac{2}{9}$，利用减法的性质$a - b - c = a-(b + c)$，可得$9.625-(\frac{16}{9}+\frac{2}{9})$，先计算$\frac{16}{9}+\frac{2}{9}=2$，再计算$9.625 - 2 = 7.625$。
3. 对于$\frac{19}{21}-\frac{5}{24}+\frac{2}{21}-\frac{7}{24}$，利用加法交换律和减法的性质，可得$(\frac{19}{21}+\frac{2}{21})-(\frac{5}{24}+\frac{7}{24})$，先计算$\frac{19}{21}+\frac{2}{21}=1$，$\frac{5}{24}+\frac{7}{24}=\frac{12}{24}=\frac{1}{2}$，再计算$1-\frac{1}{2}=\frac{1}{2}$。
【答案】：
1. $1\frac{5}{17}$
2. $7.625$
3. $\frac{1}{2}$

二、找朋友。(连一连)

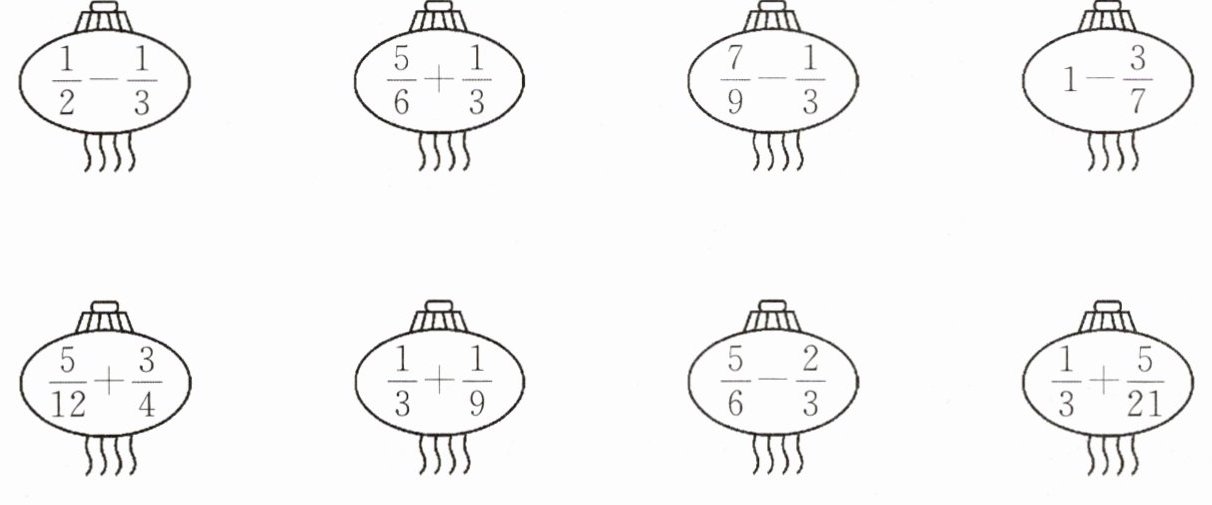
答案： 【解析】：由于你没有给出具体的“找朋友”的内容，无法进行详细解析。一般来说，“找朋友”这类题目是要根据一定的规则或特征，将相关的事物进行连线匹配，比如可能是根据数值相等、概念对应、运算结果相同等规则。
【答案】：请你补充具体的连线内容，以便我给出准确答案。