2025年暑假生活海燕出版社五年级数学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年暑假生活海燕出版社五年级数学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
4. 计算下面各题。
$\frac {7}{8}-\frac {3}{5}+\frac {1}{8}$ $\frac {1}{2}+(\frac {5}{6}-\frac {3}{4})$ $\frac {7}{5}-1+\frac {2}{15}$ $\frac {5}{6}-(\frac {2}{3}+\frac {1}{6})$
$\frac {7}{8}-\frac {3}{5}+\frac {1}{8}$ $\frac {1}{2}+(\frac {5}{6}-\frac {3}{4})$ $\frac {7}{5}-1+\frac {2}{15}$ $\frac {5}{6}-(\frac {2}{3}+\frac {1}{6})$
答案:
【解析】:
1. 计算$\frac{7}{8}-\frac{3}{5}+\frac{1}{8}$:
根据加法交换律$a - b + c=a + c - b$,将式子变形为$\frac{7}{8}+\frac{1}{8}-\frac{3}{5}$。
先计算$\frac{7}{8}+\frac{1}{8}=\frac{7 + 1}{8}=1$,再计算$1-\frac{3}{5}=\frac{5}{5}-\frac{3}{5}=\frac{5 - 3}{5}=\frac{2}{5}$。
2. 计算$\frac{1}{2}+(\frac{5}{6}-\frac{3}{4})$:
先算括号里的$\frac{5}{6}-\frac{3}{4}$,通分,$6$和$4$的最小公倍数是$12$,则$\frac{5}{6}-\frac{3}{4}=\frac{5×2}{6×2}-\frac{3×3}{4×3}=\frac{10}{12}-\frac{9}{12}=\frac{10 - 9}{12}=\frac{1}{12}$。
再算$\frac{1}{2}+\frac{1}{12}$,通分,$2$和$12$的最小公倍数是$12$,$\frac{1}{2}+\frac{1}{12}=\frac{1×6}{2×6}+\frac{1}{12}=\frac{6}{12}+\frac{1}{12}=\frac{6 + 1}{12}=\frac{7}{12}$。
3. 计算$\frac{7}{5}-1+\frac{2}{15}$:
把$1$化为$\frac{5}{5}$,则$\frac{7}{5}-1+\frac{2}{15}=\frac{7}{5}-\frac{5}{5}+\frac{2}{15}$。
先算$\frac{7}{5}-\frac{5}{5}=\frac{7 - 5}{5}=\frac{2}{5}$,再算$\frac{2}{5}+\frac{2}{15}$,通分,$5$和$15$的最小公倍数是$15$,$\frac{2}{5}+\frac{2}{15}=\frac{2×3}{5×3}+\frac{2}{15}=\frac{6}{15}+\frac{2}{15}=\frac{6 + 2}{15}=\frac{8}{15}$。
4. 计算$\frac{5}{6}-(\frac{2}{3}+\frac{1}{6})$:
去括号得$\frac{5}{6}-\frac{2}{3}-\frac{1}{6}$,根据交换律变形为$\frac{5}{6}-\frac{1}{6}-\frac{2}{3}$。
先算$\frac{5}{6}-\frac{1}{6}=\frac{5 - 1}{6}=\frac{4}{6}=\frac{2}{3}$,再算$\frac{2}{3}-\frac{2}{3}=0$。
【答案】:$\frac{2}{5}$,$\frac{7}{12}$,$\frac{8}{15}$,$0$
1. 计算$\frac{7}{8}-\frac{3}{5}+\frac{1}{8}$:
根据加法交换律$a - b + c=a + c - b$,将式子变形为$\frac{7}{8}+\frac{1}{8}-\frac{3}{5}$。
先计算$\frac{7}{8}+\frac{1}{8}=\frac{7 + 1}{8}=1$,再计算$1-\frac{3}{5}=\frac{5}{5}-\frac{3}{5}=\frac{5 - 3}{5}=\frac{2}{5}$。
2. 计算$\frac{1}{2}+(\frac{5}{6}-\frac{3}{4})$:
先算括号里的$\frac{5}{6}-\frac{3}{4}$,通分,$6$和$4$的最小公倍数是$12$,则$\frac{5}{6}-\frac{3}{4}=\frac{5×2}{6×2}-\frac{3×3}{4×3}=\frac{10}{12}-\frac{9}{12}=\frac{10 - 9}{12}=\frac{1}{12}$。
再算$\frac{1}{2}+\frac{1}{12}$,通分,$2$和$12$的最小公倍数是$12$,$\frac{1}{2}+\frac{1}{12}=\frac{1×6}{2×6}+\frac{1}{12}=\frac{6}{12}+\frac{1}{12}=\frac{6 + 1}{12}=\frac{7}{12}$。
3. 计算$\frac{7}{5}-1+\frac{2}{15}$:
把$1$化为$\frac{5}{5}$,则$\frac{7}{5}-1+\frac{2}{15}=\frac{7}{5}-\frac{5}{5}+\frac{2}{15}$。
先算$\frac{7}{5}-\frac{5}{5}=\frac{7 - 5}{5}=\frac{2}{5}$,再算$\frac{2}{5}+\frac{2}{15}$,通分,$5$和$15$的最小公倍数是$15$,$\frac{2}{5}+\frac{2}{15}=\frac{2×3}{5×3}+\frac{2}{15}=\frac{6}{15}+\frac{2}{15}=\frac{6 + 2}{15}=\frac{8}{15}$。
4. 计算$\frac{5}{6}-(\frac{2}{3}+\frac{1}{6})$:
去括号得$\frac{5}{6}-\frac{2}{3}-\frac{1}{6}$,根据交换律变形为$\frac{5}{6}-\frac{1}{6}-\frac{2}{3}$。
先算$\frac{5}{6}-\frac{1}{6}=\frac{5 - 1}{6}=\frac{4}{6}=\frac{2}{3}$,再算$\frac{2}{3}-\frac{2}{3}=0$。
【答案】:$\frac{2}{5}$,$\frac{7}{12}$,$\frac{8}{15}$,$0$
5. 放学后,小明从学校回家,他走了$\frac {2}{5}km$,再走$\frac {1}{3}km$就到了家与学校的中点处,小明家距离学校有多远?
答案:
【解析】:本题可先求出从学校到家的中点的距离,再根据中点的性质求出小明家到学校的距离。
已知小明走了$\frac{2}{5}km$,再走$\frac{1}{3}km$就到了家与学校的中点处,那么从学校到中点的距离是已经走的路程加上还需走的路程,即$(\frac{2}{5} + \frac{1}{3})km$。
因为中点到学校的距离与中点到家的距离相等,所以小明家到学校的距离是从学校到中点距离的$2$倍,则小明家到学校的距离为$2×(\frac{2}{5} + \frac{1}{3})$千米。
计算$2×(\frac{2}{5} + \frac{1}{3})$时,先算括号内的加法,再算括号外的乘法。
$\frac{2}{5} + \frac{1}{3}=\frac{6}{15} + \frac{5}{15}=\frac{11}{15}$(千米)
$2×\frac{11}{15}=\frac{22}{15}$(千米)
【答案】:$\frac{22}{15}km$
已知小明走了$\frac{2}{5}km$,再走$\frac{1}{3}km$就到了家与学校的中点处,那么从学校到中点的距离是已经走的路程加上还需走的路程,即$(\frac{2}{5} + \frac{1}{3})km$。
因为中点到学校的距离与中点到家的距离相等,所以小明家到学校的距离是从学校到中点距离的$2$倍,则小明家到学校的距离为$2×(\frac{2}{5} + \frac{1}{3})$千米。
计算$2×(\frac{2}{5} + \frac{1}{3})$时,先算括号内的加法,再算括号外的乘法。
$\frac{2}{5} + \frac{1}{3}=\frac{6}{15} + \frac{5}{15}=\frac{11}{15}$(千米)
$2×\frac{11}{15}=\frac{22}{15}$(千米)
【答案】:$\frac{22}{15}km$
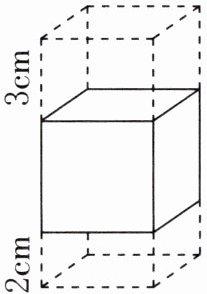
6. 如下图,一个长方体木块,从下部和上部分别截去高是2cm和3cm的长方体后变成了一个正方体,表面积减少了$120cm^2。$原来长方体木块的体积是多少立方厘米?

答案:
【解析】:
- 分析表面积减少的部分:
截去上下两个长方体后,表面积减少的部分是$4$个相同的以原来长方体底面边长为长,$(2 + 3)$cm为宽的长方形的面积之和。
已知表面积减少了$120cm^{2}$,那么一个这样的长方形面积是$120÷4 = 30cm^{2}$。
又因为这个长方形的宽是$2 + 3 = 5cm$,所以长方形的长(即正方体的棱长)为$30÷5 = 6cm$。
计算原来长方体的高:
正方体棱长为$6cm$,原来长方体的高是$6 + 2 + 3 = 11cm$。
计算原来长方体的体积:
根据长方体体积公式$V=a× b× h$(这里$a = b = 6cm$,$h = 11cm$),可得体积$V = 6×6×11 = 396cm^{3}$。
【答案】:$396$
- 分析表面积减少的部分:
截去上下两个长方体后,表面积减少的部分是$4$个相同的以原来长方体底面边长为长,$(2 + 3)$cm为宽的长方形的面积之和。
已知表面积减少了$120cm^{2}$,那么一个这样的长方形面积是$120÷4 = 30cm^{2}$。
又因为这个长方形的宽是$2 + 3 = 5cm$,所以长方形的长(即正方体的棱长)为$30÷5 = 6cm$。
计算原来长方体的高:
正方体棱长为$6cm$,原来长方体的高是$6 + 2 + 3 = 11cm$。
计算原来长方体的体积:
根据长方体体积公式$V=a× b× h$(这里$a = b = 6cm$,$h = 11cm$),可得体积$V = 6×6×11 = 396cm^{3}$。
【答案】:$396$
7. 某市要挖一个长50m、宽20m、深1.5m的游泳池,施工团队使用的挖土机每小时可挖土$24m^3,$如果每天工作8小时,至少要多少天才可以完成挖土工程?
答案:
【解析】:本题可先根据长方体的体积公式求出游泳池的容积,也就是需要挖土的体积,再计算出挖土机每天挖土的体积,最后用需要挖土的总体积除以挖土机每天挖土的体积,得到需要的天数,若结果不是整数则需向上取整。
- **步骤一:计算游泳池的容积(即挖土的体积)**
根据长方体的体积公式$V = a× b× h$(其中$V$为长方体体积,$a$为长,$b$为宽,$h$为高),已知游泳池长$50m$、宽$20m$、深$1.5m$,可得游泳池的容积为:
$50×20×1.5 = 1500(m^3)$
- **步骤二:计算挖土机每天挖土的体积**
已知挖土机每小时可挖土$24m^3$,每天工作$8$小时,根据“每天挖土体积$=$每小时挖土体积$×$每天工作时间”,可得挖土机每天挖土的体积为:
$24×8 = 192(m^3)$
- **步骤三:计算完成挖土工程需要的天数**
用需要挖土的总体积除以挖土机每天挖土的体积,可得需要的天数为:
$1500÷192 = 7.8125$(天)
由于天数必须为整数,且$7$天无法完成任务,所以需要向上取整,即至少需要$8$天才能完成挖土工程。
【答案】:$8$
- **步骤一:计算游泳池的容积(即挖土的体积)**
根据长方体的体积公式$V = a× b× h$(其中$V$为长方体体积,$a$为长,$b$为宽,$h$为高),已知游泳池长$50m$、宽$20m$、深$1.5m$,可得游泳池的容积为:
$50×20×1.5 = 1500(m^3)$
- **步骤二:计算挖土机每天挖土的体积**
已知挖土机每小时可挖土$24m^3$,每天工作$8$小时,根据“每天挖土体积$=$每小时挖土体积$×$每天工作时间”,可得挖土机每天挖土的体积为:
$24×8 = 192(m^3)$
- **步骤三:计算完成挖土工程需要的天数**
用需要挖土的总体积除以挖土机每天挖土的体积,可得需要的天数为:
$1500÷192 = 7.8125$(天)
由于天数必须为整数,且$7$天无法完成任务,所以需要向上取整,即至少需要$8$天才能完成挖土工程。
【答案】:$8$
查看更多完整答案,请扫码查看


