《2025年暑假生活海燕出版社五年级数学人教版》

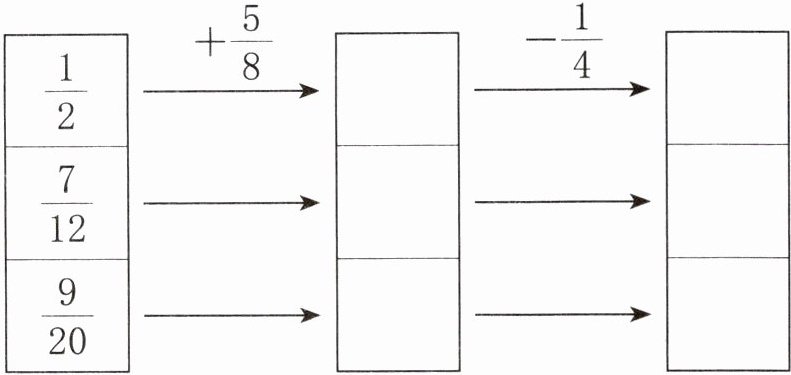
4. 算一算,填一填。

答案： 【解析】：
- 对于$\frac{1}{2}+\frac{5}{8}$：先通分，$2$和$8$的最小公倍数是$8$，$\frac{1}{2}=\frac{1×4}{2×4}=\frac{4}{8}$，则$\frac{1}{2}+\frac{5}{8}=\frac{4}{8}+\frac{5}{8}=\frac{9}{8}$；再计算$\frac{9}{8}-\frac{1}{4}$，$4$和$8$的最小公倍数是$8$，$\frac{1}{4}=\frac{1×2}{4×2}=\frac{2}{8}$，所以$\frac{9}{8}-\frac{1}{4}=\frac{9}{8}-\frac{2}{8}=\frac{7}{8}$。
- 对于$\frac{7}{12}+\frac{5}{8}$：$12$和$8$的最小公倍数是$24$，$\frac{7}{12}=\frac{7×2}{12×2}=\frac{14}{24}$，$\frac{5}{8}=\frac{5×3}{8×3}=\frac{15}{24}$，则$\frac{7}{12}+\frac{5}{8}=\frac{14}{24}+\frac{15}{24}=\frac{29}{24}$；接着计算$\frac{29}{24}-\frac{1}{4}$，$\frac{1}{4}=\frac{1×6}{4×6}=\frac{6}{24}$，所以$\frac{29}{24}-\frac{1}{4}=\frac{29}{24}-\frac{6}{24}=\frac{23}{24}$。
- 对于$\frac{9}{20}+\frac{5}{8}$：$20$和$8$的最小公倍数是$40$，$\frac{9}{20}=\frac{9×2}{20×2}=\frac{18}{40}$，$\frac{5}{8}=\frac{5×5}{8×5}=\frac{25}{40}$，则$\frac{9}{20}+\frac{5}{8}=\frac{18}{40}+\frac{25}{40}=\frac{43}{40}$；然后计算$\frac{43}{40}-\frac{1}{4}$，$\frac{1}{4}=\frac{1×10}{4×10}=\frac{10}{40}$，所以$\frac{43}{40}-\frac{1}{4}=\frac{43}{40}-\frac{10}{40}=\frac{33}{40}$。
【答案】：$\frac{9}{8}$，$\frac{7}{8}$；$\frac{29}{24}$，$\frac{23}{24}$；$\frac{43}{40}$，$\frac{33}{40}$。

5. 水果店购进一批橙子,第一天卖了它的$\frac {1}{6}$,第二天卖了它的$\frac {5}{9}$。还剩下几分之几？

答案： 【解析】：把这批橙子看作单位“1”，用单位“1”依次减去第一天和第二天卖出的分率，即可求出剩下的分率。列式为$1-\frac{1}{6}-\frac{5}{9}$，先通分，$1=\frac{18}{18}$，$\frac{1}{6}=\frac{3}{18}$，$\frac{5}{9}=\frac{10}{18}$，则$1-\frac{1}{6}-\frac{5}{9}=\frac{18}{18}-\frac{3}{18}-\frac{10}{18}=\frac{18 - 3 - 10}{18}=\frac{5}{18}$。
【答案】：$\frac{5}{18}$

6. 一杯咖啡,李叔叔喝了$\frac {3}{5}$杯后,觉得有点苦,就兑满牛奶,搅拌均匀后,又喝了半杯,就出去工作了。李叔叔一共喝了多少杯咖啡,多少杯牛奶？(画一画,写一写)

答案： 【解析】：
1. 首先分析第一次喝咖啡的量：
李叔叔一开始喝了$\frac{3}{5}$杯咖啡，此时杯中还剩下的咖啡为$1 - \frac{3}{5}=\frac{2}{5}$杯。
2. 然后兑满牛奶，此时杯子里液体总量还是$1$杯，其中咖啡占$\frac{2}{5}$杯，牛奶占$1-\frac{2}{5}=\frac{3}{5}$杯。
3. 接着分析第二次喝的情况：
又喝了半杯，即$\frac{1}{2}$杯。这$\frac{1}{2}$杯里咖啡的量为$\frac{2}{5}×\frac{1}{2}=\frac{1}{5}$杯，牛奶的量为$\frac{3}{5}×\frac{1}{2}=\frac{3}{10}$杯。
4. 最后计算总共喝的咖啡和牛奶的量：
总共喝的咖啡量是第一次喝的咖啡量加上第二次喝的咖啡量，即$\frac{3}{5}+\frac{1}{5}=\frac{3 + 1}{5}=\frac{4}{5}$杯。
总共喝的牛奶量就是第二次喝的牛奶量，为$\frac{3}{10}$杯。
【答案】：$\frac{4}{5}$；$\frac{3}{10}$

7. 古埃及人非常喜欢分子是1的分数,比如$\frac {1}{5}$,$\frac {1}{8}$,因此这样的分数也叫埃及分数。他们会把$\frac {2}{101}分解为\frac {1}{101}+\frac {1}{202}+\frac {1}{303}+\frac {1}{606}$。古埃及人把9个橙子分给10人,每人可以分到$(\frac {1}{3}+\frac {1}{4}+\frac {1}{5}+\frac {1}{12}+\frac {1}{30})$个橙子。生活中我们会碰到“把6个同样大小的苹果平均分给8个孩子,可以怎样分？每个孩子分得这些苹果的几分之几”这样的问题,我们可以先将4个苹果平均分给8人,每人分得$\frac {1}{2}$个；再将剩下的2个平均分给8人,每人分得$\frac {1}{4}$个。所以每人分得$\frac {1}{2}+\frac {1}{4}= \frac {3}{4}$(个),这就是埃及分数在实际中的应用了。
如果让你把7个完全一样的小蛋糕平均分给12个小朋友,你会怎样分呢？每个小朋友能分到这些蛋糕的几分之几呢？试着分分看。

答案： 【解析】：我们可以先把其中一部分蛋糕平均分给$12$个小朋友，算出每人分得的量，再把剩下的蛋糕也平均分给$12$个小朋友，算出每人分得的量，最后把两次每人分得的量相加，就是每个小朋友最终分得的量。同时，把$7$个蛋糕看作单位“$1$”，平均分给$12$个小朋友，每人分得这些蛋糕的$\frac{1}{12}$。
先将$3$个蛋糕平均分给$12$人，每人分得$3÷12 = \frac{1}{4}$个；再将剩下的$4$个蛋糕平均分给$12$人，每人分得$4÷12=\frac{1}{3}$个。所以每人分得$\frac{1}{3}+\frac{1}{4}=\frac{4 + 3}{12}=\frac{7}{12}$个。
【答案】：先将$3$个蛋糕平均分给$12$人，每人分得$\frac{1}{4}$个；再将剩下的$4$个蛋糕平均分给$12$人，每人分得$\frac{1}{3}$个，每个小朋友能分到$\frac{7}{12}$个蛋糕，每个小朋友能分到这些蛋糕的$\frac{1}{12}$。