《2025年暑假大串联安徽人民出版社八年级数学北师大版》

23. 某市为了鼓励居民节约用电,采用分段计费的方法按月计算每户家庭的电费。月用电量不超过 200 度时,按 0.55 元/度计费；月用电量超过 200 度时,其中的 200 度仍按 0.55 元/度计费,超过部分按 0.70 元/度计费。设每户家庭月用电量为 $ x $ 度时,应交电费 $ y $ 元。
(1)分别求出 $ 0\leqslant x\leqslant 200 $ 和 $ x＞200 $ 时,$ y $ 与 $ x $ 的关系式；
(2)王冬家 5 月份交电费 117 元,王冬家这个月用电多少度？

答案： 解：
(1)当 $ 0 \leqslant x \leqslant 200 $ 时，$ y $ 与 $ x $ 的关系式是 $ y = 0.55 x $;
当 $ x ＞ 200 $ 时，$ y $ 与 $ x $ 的关系式是 $ y = 0.55 \times 200 + 0.7 ( x - 200 ) $，即 $ y = 0.7 x - 30 $.
(2)$ \because $王冬家 5 月份的电费超过 110 元，
$ \therefore $把 $ y = 117 $ 代入 $ y = 0.7 x - 30 $ 中，得 $ x = 210 $.
答：王冬家 5 月份用电 210 度.

24. 认真阅读下面关于三角形内外角平分线所夹的角的探究片段,完成所提出的问题。
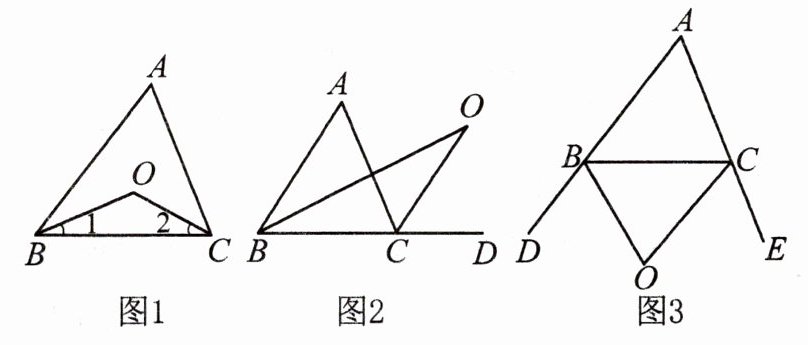
探究 1：如图 1,在 $ △ABC $ 中,$ O $ 是 $ ∠ABC $ 与 $ ∠ACB $ 的平分线 $ BO $ 和 $ CO $ 的交点,通过分析发现 $ ∠BOC= 90^{\circ}+\frac{1}{2}∠A $,理由如下：
∵ $ BO $ 和 $ CO $ 分别是 $ ∠ABC $ 和 $ ∠ACB $ 的角平分线,
∴ $ ∠1= \frac{1}{2}∠ABC $,$ ∠2= \frac{1}{2}∠ACB $,
∴ $ ∠1+∠2= \frac{1}{2}(∠ABC+∠ACB) $。
又∵ $ ∠ABC+∠ACB= 180^{\circ}-∠A $,
∴ $ ∠1+∠2= \frac{1}{2}(180^{\circ}-∠A)= 90^{\circ}-\frac{1}{2}∠A $,
∴ $ ∠BOC= 180^{\circ}-(∠1+∠2)= 180^{\circ}-(90^{\circ}-\frac{1}{2}∠A)= 90^{\circ}+\frac{1}{2}∠A $。
探究 2：如图 2 中,$ O $ 是 $ ∠ABC $ 与外角 $ ∠ACD $ 的平分线 $ BO $ 和 $ CO $ 的交点,试分析 $ ∠BOC $ 与 $ ∠A $ 有怎样的关系？请说明理由。
探究 3：如图 3 中,$ O $ 是外角 $ ∠DBC $ 与外角 $ ∠ECB $ 的平分线 $ BO $ 和 $ CO $ 的交点,则 $ ∠BOC $ 与 $ ∠A $ 有怎样的关系？(只写结论,不需证明)
结论：______。

答案：
解：探究 2 结论：$ \angle B O C = \frac { 1 } { 2 } \angle A $.
理由如下：
$ \because $如图，$ B O $ 和 $ C O $ 分别是 $ \angle A B C $ 和 $ \angle A C D $ 的角平分线，
$ \therefore \angle 1 = \frac { 1 } { 2 } \angle A B C $，$ \angle 2 = \frac { 1 } { 2 } \angle A C D $.
又 $ \because \angle A C D $ 是 $ \triangle A B C $ 的一个外角，
$ \therefore \angle A C D = \angle A + \angle A B C $,
$ \therefore \angle 2 = \frac { 1 } { 2 } ( \angle A + \angle A B C ) = \frac { 1 } { 2 } \angle A + \angle 1 $.
$ \because \angle 2 $ 是 $ \triangle B O C $ 的一个外角，
$ \therefore \angle B O C = \angle 2 - \angle 1 = \frac { 1 } { 2 } \angle A + \angle 1 - \angle 1 = \frac { 1 } { 2 } \angle A $;

探究 3：$ \angle B O C = 90 ^ { \circ } - \frac { 1 } { 2 } \angle A $.