《2025年暑假大串联安徽人民出版社八年级数学北师大版》

2. (苏州中考题)如图,在△ABC中,点D在BC上,AB = AD = DC,∠B = 80°,则∠C的度数为()

A. 30°
B. 40°
C. 45°
D. 60°

答案： B

3. (滨州中考题)下列四组线段中,可以构成直角三角形的是()
A. 5,6,7
B. 3,4,5
C. 4,5,6
D. √3,2,√5

答案： B

4. (安徽中考题)如图,Rt△ABC中,AB = 9,BC = 6,∠B = 90°,将△ABC折叠,使A点与BC的中点D重合,折痕为MN,则线段BN的长为()

A. 5/3
B. 5/2
C. 4
D. 5

答案： C

5. (咸宁中考题)如图,l//m,等边△ABC的顶点B在直线m上,∠1 = 20°,则∠2的度数为()

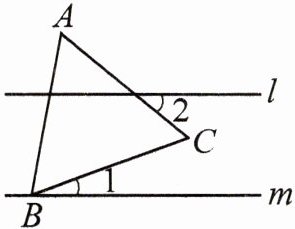
A. 60°
B. 45°
C. 40°
D. 30°

答案： C

6. (绍兴中考题)问题：如图,在△ABD中,BA = BD. 在BD的延长线上取点E,C,作△AEC,使EA = EC. 若∠BAE = 90°,∠B = 45°,求∠DAC的度数.
答案：∠DAC = 45°.


思考：
(1)如果把以上“问题”中的条件“∠B = 45°”去掉,其余条件不变,那么∠DAC的度数会改变吗？说明理由；
(2)如果把以上“问题”中的条件“∠B = 45°”去掉,再将“∠BAE = 90°”改为“∠BAE = n°”,其余条件不变,求∠DAC的度数.

答案：
(1)∠DAC的度数不会改变,
　
∵EA=EC,
　
∴∠EAC=∠C　①.
　
∵BA=BD,
　
∴∠BAD=∠BDA.
　
∵∠BAE=90°,
　
∴∠B=90°−∠AED=90°−2∠C,
　
∴∠BAD=$\frac{1}{2}$(180°−∠B)=$\frac{1}{2}$[180°−(90°−2∠C)]=45°+∠C,
　
∴∠DAE=90°−∠BAD=90°−(45°+∠C)=45°−∠C　②,
　　由①②得,∠DAC=∠DAE+∠CAE =45°−∠C+∠C=45°.
(2)设∠ABC=m°,则∠BAD=$\frac{1}{2}$(180°−m°)=90°−$\frac{1}{2}$m°,∠AEB=180°−n°−m°,
∴∠DAE=n°−∠BAD=n°−90°+$\frac{1}{2}$m°.
∵EA=EC,
∴∠CAE=$\frac{1}{2}$∠AEB = 90°−$\frac{1}{2}$n°−$\frac{1}{2}$m°,
　
∴∠DAC=∠DAE+∠CAE=n°−90°+$\frac{1}{2}$m°+90°−$\frac{1}{2}$n°−$\frac{1}{2}$m°=$\frac{1}{2}$n°.