《2025年暑假大串联安徽人民出版社八年级数学北师大版》

1. (无锡中考题)函数$y= \sqrt {2-x}$中自变量x的取值范围是 ()
A. $x＞2$
B. $x≥2$
C. $x≤2$
D. $x≠2$

答案： C

2. (锦州中考题)已知$a＞b＞0$,下列结论错误的是 ()
A. $a+m＞b+m$
B. $\sqrt {a}＞\sqrt {b}$
C. $-2a＞-2b$
D. $\frac {a}{2}＞\frac {b}{2}$

答案： C

3. (玉林中考题)在数轴上表示不等式$x+5≥1$的解集,正确的是 ()

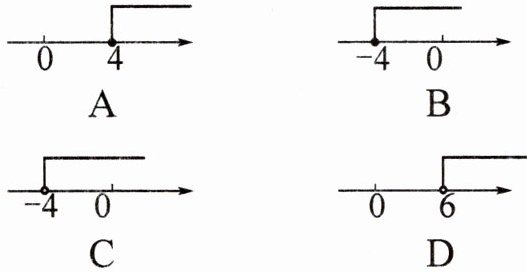
答案： B

4. (甘孜州中考题)不等式$3x-2＞4$的解集为____.

答案： $x＞2$

5. (铜仁中考题)不等式$2m-1≤6$的正整数解是____.

答案： $1$，$2$，$3$

6. (西宁中考题)解不等式组$\left\{\begin{array}{l} 2x-2≤x,\\ x+2＞-\frac {1}{2}x-1,\end{array}\right.$并把解集在数轴上表示出来.

答案：
解：$\begin{cases}2x - 2≤x & ①\\x + 2＞-\frac{1}{2}x - 1 & ②\end{cases}$，
解不等式①，得$x≤2$，
解不等式②，得$x＞-2$，
∴不等式组的解集是$-2＜x≤2$。
把不等式组的解集在数轴上表示出来为：

7. (嘉兴中考题)某汽车专卖店销售A,B两种型号的新能源汽车,上周售出1辆A型车和3辆B型车,销售额为96万元；本周已售2辆A型车和1辆B型车,销售额为62万元.
(1)求每辆A型车和B型车的售价各多少万元.
(2)甲公司拟向该店购买A,B两种型号的新能源汽车共6辆,购车费不少于130万元,且不超过140万元,则有哪几种购车方案?

答案： 解：（1）设每辆$A$型车的售价为$x$万元，每辆$B$型车的售价为$y$万元。根据题意，得：
$\begin{cases}x + 3y = 96\\2x + y = 62\end{cases}$，解得$\begin{cases}x = 18\\y = 26\end{cases}$。
答：每辆$A$型车的售价为$18$万元，每辆$B$型车的售价为$26$万元。
（2）设购买$A$型车$a$辆，则购买$B$型车$(6 - a)$辆。根据题意，得：
$\begin{cases}18a + 26(6 - a)≥130\\18a + 26(6 - a)≤140\end{cases}$，
解得$2≤a≤3\frac{1}{4}$。
∵$a$是正整数，
∴$a = 2$，或$a = 3$。
∴共有两种方案。
方案一：购买$2$辆$A$型车和$4$辆$B$型车。
方案二：购买$3$辆$A$型车和$3$辆$B$型车。