《2025年暑假大串联安徽人民出版社八年级数学北师大版》

20. 先化简,再求值：$-2(mn - 3m^{2}) - [m^{2}-5(mn - m^{2}) + 2mn]$,其中$m = 1$,$n = -2$.

答案： 解：原式$= - 2mn + 6m^{2} - m^{2} + 5(mn - m^{2}) - 2mn = - 2mn + 6m^{2} - m^{2} + 5mn - 5m^{2} - 2mn = mn$，
当$m = 1$，$n = - 2$时，原式$= 1×(- 2) = - 2$。

21. (1)如图,已知点$C在线段AB$上,且$AC = 6cm$,$BC = 4cm$,点$M$,$N分别是AC$,$BC$的中点,求线段$MN$的长度；


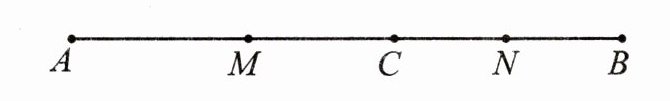
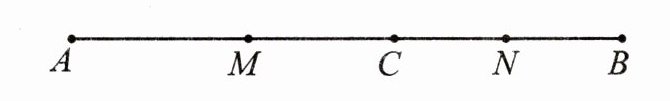
(2)若点$C是线段AB$上任意一点,且$AC = a$,$BC = b$,点$M$,$N分别是AC$,$BC$的中点,请直接写出线段$MN$的长度；(用含$a$,$b$的代数式表示)
(3)在(2)中,把“点$C是线段AB$上任意一点”改为“点$C是直线AB$上任意一点”,其他条件不变,则线段$MN$的长度会变化吗？若有变化,求出结果.

答案：
解：
(1)
∵$AC = 6cm$，点$M$是$AC$的中点，
∴$CM = \frac{1}{2}AC = 3cm$。
∵$BC = 4cm$，点$N$是$BC$的中点，
∴$CN = \frac{1}{2}BC = 2cm$，
∴$MN = CM + CN = 5cm$。
∴线段$MN$的长度为$5cm$。
(2)$MN = \frac{a + b}{2}$；
(3)线段$MN$的长度会变化。
当点$C$在线段$AB$上时，由
(2)知$MN = \frac{a + b}{2}$；
当点$C$在线段$AB$的延长线上时，如图：
则$AC = a＞BC = b$。
∵$AC = a$，点$M$是$AC$的中点，
∴$CM = \frac{1}{2}AC = \frac{1}{2}a$。
∵$BC = b$，点$N$是$BC$的中点，
∴$CN = \frac{1}{2}BC = \frac{1}{2}b$，
∴$MN = CM - CN = \frac{a - b}{2}$。
当点$C$在线段$BA$的延长线上时，如图：

则$AC = a＜BC = b$。
同理可求：$CM = \frac{1}{2}AC = \frac{1}{2}a$，$CN = \frac{1}{2}BC = \frac{1}{2}b$，
∴$MN = CN - CM = \frac{b - a}{2}$。
∴综上所述，线段$MN$的长度会变化，$MN = \frac{a + b}{2}$，$\frac{a - b}{2}$或$\frac{b - a}{2}$。

22. $2020年11月20$日,深圳第六次获得“全国文明城市”称号.“来了就是深圳人,来了就是志愿者”,如今深圳活跃着$208$万“红马甲”志愿者,共同服务深圳.某校随机抽取了部分学生对志愿服务活动情况进行如下调查：$A$.未参加过志愿服务活动；$B$.参加志愿服务活动$1$次；$C$.参加志愿服务活动$2$次；$D$.参加志愿服务活动$3$次及以上；并将调查结果绘制成了两幅不完整的统计图,请你根据图中提供的信息回答以下问题：


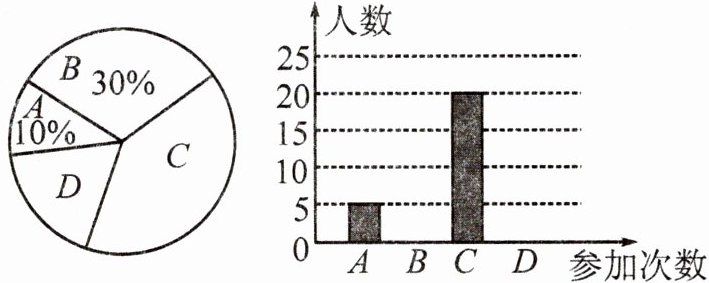
(1)共调查了______名学生；
(2)补全条形统计图；
(3)计算扇形统计图中“参加志愿服务活动$2$次”部分所对应的圆心角的度数为______；
(4)该校共有$1200$名学生,估计“参加志愿服务活动$3$次及以上”的学生大约有多少名？

答案：
解：
(1)$5÷10\% = 50$（人），故答案为：50；
(2)“B. 参加志愿服务活动1次”的人数为：$50×30\% = 15$（人），
“D. 参加志愿服务活动3次及以上”的人数为：$50 - 5 - 15 - 20 = 10$（人），
补全条形统计图如图所示：

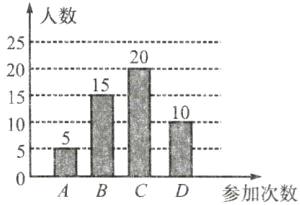
(3)$360^{\circ}×\frac{20}{50} = 144^{\circ}$，故答案为：$144^{\circ}$；
(4)$1200×\frac{10}{50} = 240$（名）。