《2025年暑假大串联安徽人民出版社八年级数学北师大版》

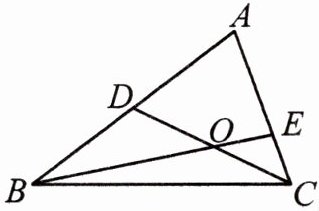
4. 如图,$D$ 为 $\triangle ABC$ 的 $AB$ 边上的中点,$E$ 为 $AC$ 上一点,$AE = 2CE$,$BE$ 与 $CD$ 交于 $O$,求证：$OE= \frac{1}{4}BE$.

答案：
证明:取$BE$的中点$F$，连接$DF$，则$EF = BF$.

$\because D$，$F$分别是$\triangle ABE$的边$AB$和$BE$的中点，
$\therefore DF// AE$，$AE = 2DF$.
$\therefore\angle ODF = \angle OCE$，$\angle OFD = \angle OEC$.
又$\because AE = 2CE$，
$\therefore DF = EC$.
$\therefore\triangle ODF\cong\triangle OCE$，
$\therefore OE = OF = \frac{1}{2}EF$，
$\therefore OE = \frac{1}{4}BE$.

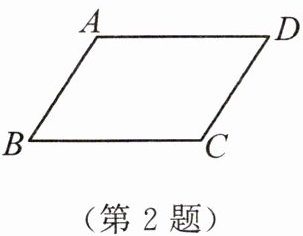
1. (广东中考题)如图,$\square ABCD$ 中,下列说法一定正确的是 ()

A. $AC = BD$ B. $AC\perp BD$
C. $AB = CD$ D. $AB = BC$

答案： C

2. (临沂中考题)将一个 $n$ 边形变成 $n + 1$ 边形,内角和将 ()

A. 减少 $180^{\circ}$
B. 增加 $90^{\circ}$
C. 增加 $180^{\circ}$
D. 增加 $360^{\circ}$

答案： C

3. (盐城中考题)如图,$A$,$B$ 两地间有一池塘阻隔,为测量 $A$,$B$ 两地的距离,在地面上选一点 $C$,连接 $CA$,$CB$ 的中点 $D$,$E$. 若 $DE$ 的长度为 $30\mathrm{m}$,则 $A$,$B$ 两地的距离为____$\mathrm{m}$.

答案： 60

4. (遂宁中考题)正多边形一个外角的度数是 $60^{\circ}$,则该正多边形的边数是____.

答案： 6

5. (深圳中考题)如图,已知 $BD$ 垂直平分 $AC$,$\angle BCD = \angle ADF$,$AF\perp AC$.
(1) 证明：四边形 $ABDF$ 是平行四边形；
(2) 若 $AF = DF = 5$,$AD = 6$,求 $AC$ 的长.

答案：
(1)证明:$\because BD$垂直平分$AC$，
$\therefore AB = BC$，$AD = DC$，
$\therefore\angle BAC = \angle BCA$，$\angle DAC = \angle DCA$，
$\therefore\angle BAD = \angle BCD$.
$\because\angle BCD = \angle ADF$，
$\therefore\angle BAD = \angle ADF$，
$\therefore AB// FD$.
$\because BD\perp AC$，$AF\perp AC$，
$\therefore AF// BD$，
$\therefore$四边形$ABDF$是平行四边形.
(2)解:$\because$四边形$ABDF$是平行四边形，
$\therefore AB = DF$，$AF = BD$.
$\because AF = DF = 5$，
$\therefore AB = BD = 5$.
设$BE = x$，则$DE = 5 - x$，
$\therefore AB^{2} - BE^{2} = AD^{2} - DE^{2}$，
即$5^{2} - x^{2} = 6^{2} - (5 - x)^{2}$，
解得:$x = \frac{7}{5}$，
$\therefore AE = \sqrt{AB^{2} - BE^{2}} = \frac{24}{5}$，
$\therefore AC = 2AE = \frac{48}{5}$.