《2025年暑假大串联安徽人民出版社八年级数学北师大版》

8. 甲、乙两车相距150千米,两车同时出发,同向而行,甲车4小时可追上乙车；相向而行,1.5小时后两车相遇,求甲、乙两车的速度.

答案： 解:设甲车的速度为x千米/时，乙车的速度为y千米/时.
则$\begin{cases}4(x - y) = 150\\1.5(x + y) = 150\end{cases}$，
解得$\begin{cases}x = 68\frac{3}{4}\\y = 31\frac{1}{4}\end{cases}$.
答:甲车的速度是$68\frac{3}{4}$千米/时，乙车的速度是$31\frac{1}{4}$千米/时.

1. 甲、乙两人同求方程$ax-by= 7$的整数解,甲求出一组解为$\left\{\begin{array}{l} x= 3,\\ y= 4,\end{array}\right. 而乙把ax-by= 7$中的7错看成1,求得一组解为$\left\{\begin{array}{l} x= 1,\\ y= 2,\end{array}\right. $试求a,b的值.

答案： 解:把$x = 3$,$y = 4$代入$ax−by = 7$中,
得$3a−4b = 7$①,
把$x = 1$,$y = 2$代入$ax−by = 1$中,得$a −2b = 1$②,
解由①②组成的方程组$\begin{cases}3a - 4b = 7\\a - 2b = 1\end{cases}$,
解得$\begin{cases}a = 5\\b = 2\end{cases}$.

2. 某镇水库的可用水量为12000万立方米,假设年降水量不变,能维持该镇16万人20年的用水量.实施城市化建设,新迁入4万人后,水库只够维持居民15年的用水量.求：
(1)年降水量为多少万立方米？每人每年平均用水量为多少立方米？
(2)政府号召节约用水,希望将水库的保用年限提高到25年,则该镇居民人均每年需节约多少立方米水才能实现目标？

答案： 解:
(1)设年降水量为x万立方米，每人每年平均用水量为y立方米,则:
$\begin{cases}12000 + 20x = 16×20y\\12000 + 15x = 20×15y\end{cases}$，
解得:$\begin{cases}x = 200\\y = 50\end{cases}$，
答:年降水量为200万立方米，每人每年平均用水量为50立方米.
(2)设该镇居民每人每年平均用水量为x立方米才能实现目标，则:
$12000 + 25×200 = 20×25x$，
解得:$x = 34$.
∴$50 - 34 = 16$.
答:该镇居民人均每年需要节约16立方米水才能实现目标.

3. 一方有难,八方支援.“新冠肺炎”疫情来袭,不仅医务人员主动请缨走向抗疫前线,众多企业也伸出援助之手,某公司用甲、乙两种货车向武汉运送爱心物资,两次满载的运输情况如表：

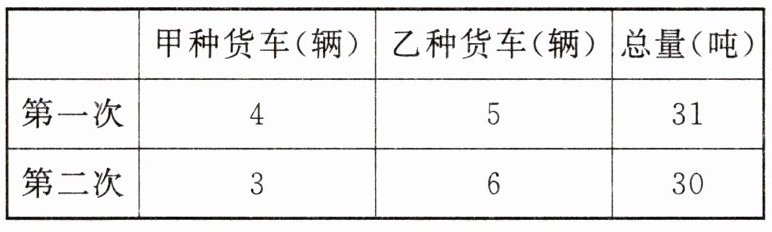
(1)甲、乙两种货车每辆分别能装货多少吨？
(2)现有45吨物资需要再次运往武汉,准备同时租用这两种货车,每辆均全部装满货物,问有哪几种租车方案？

答案： 解:
(1)设甲种货车每辆能装货x吨，乙种货车每辆能装货y吨，
依题意得$\begin{cases}4x + 5y = 33\\4x + 3y = 25\end{cases}$，解得$\begin{cases}x = 4\\y = 3\end{cases}$，答:甲种货车每辆能装货4吨，乙种货车每辆能装货3吨.
(2)设租用甲种货车m辆,乙种货车n辆，
依题意得:4m + 3n = 45,
∴$n = 15 - \frac{4}{3}m$.
又
∵m,n均为正整数，
∴$\begin{cases}m = 3\\n = 11\end{cases}$或$\begin{cases}m = 6\\n = 7\end{cases}$或$\begin{cases}m = 9\\n = 3\end{cases}$.
∴共有3种租车方案，
方案1:租用3辆甲种货车，11辆乙种货车;
方案2:租用6辆甲种货车,7辆乙种货车;
方案3:租用9辆甲种货车,3辆乙种货车