2025年教材课本高中数学选择性必修第二册人教B版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年教材课本高中数学选择性必修第二册人教B版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第74页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
4.2.3 二项分布与超几何分布
情境与问题
为了增加系统的可靠性,人们经常使用“备用冗余设备”(即正在使用的设备出故障时才启动的设备). 已知某计算机网络的服务器采用的是“一用两备”(即一台正常设备,两台备用设备)的配置,这三台设备中,只要有一台能正常工作,计算机网络就不会断掉. 如果三台设备各自能正常工作的概率都为0.9,它们之间相互不影响,那么这个计算机网络不会断掉的概率是多少呢?
情境中的问题,利用本节所要学习的知识,可以快速地得到解决.
1. n次独立重复试验与二项分布
我们已经知道,一个伯努利试验是试验结果可记为“成功”与“不成功”的试验. 现实生活中,经常需要在相同的条件下将一个伯努利试验重复多次. 例如,为了了解抛硬币时出现的统计规律,可多次重复进行抛硬币这个伯努利试验;为了了解支持改革的人的比例,可随机向多人进行访问,询问他们的态度是“支持”还是“不支持”;等等. 在相同条件下重复n次伯努利试验时,人们总是约定这n次试验是相互独立的,此时这n次伯努利试验也常称为n次独立重复试验.
例如,对一批产品进行抽样检查,每次取一件来判断是否合格,有放回地抽取5次,就是一个5次独立重复试验;篮球运动员练习投篮10次,可以认为每次投中的概率都相同,这是一个10次独立重复试验.
在n次独立重复试验中,人们经常关心的是“成功”出现的次数.
尝试与发现
已知某种药物对某种疾病的治愈率为43,现有甲、乙、丙、丁4个患有该病的患者服用了这种药物,观察其中有多少患者会被这种药物治愈.
(1)这能否看成独立重复试验?
(2)求出甲、乙、丙都被治愈而丁没被治愈的概率;
(3)求出恰有3个患者被治愈的概率;
(4)设有X人被治愈,求X的分布列.
不难想到,4个患者是否会被治愈是相互独立的,因此尝试与发现中的情形可以看成4次独立重复试验.
如果用A1,A2,A3,A4分别表示甲被治愈、乙被治愈、丙被治愈、丁被治愈,则不难看出
P(Ai)=43,P(Ai)=1−P(Ai)=41,i=1,2,3,4.
此时,甲、乙、丙都被治愈而丁没被治愈可以表示为A1A2A3A4,因此由独立性可知
P(A1A2A3A4)=P(A1)P(A2)P(A3)P(A4)
=43×43×43×41=25627.
注意到恰有3个患者被治愈的情况共有C43种(4个人中,选出3个是被治愈的,剩下的那个是没被治愈的),即
A1A2A3A4,A1A2A3A4,A1A2A3A4,A1A2A3A4,
这四种情况两两都是互斥的,而且每一种情况的概率均为(43)3×41=25627,因此所求概率为
P(A1A2A3A4+A1A2A3A4+A1A2A3A4+A1A2A3A4)
=P(A1A2A3A4)+P(A1A2A3A4)+P(A1A2A3A4)+P(A1A2A3A4)
=C43×(43)3×41=6427.
因为共有4名患者服用了药物,所以X的取值范围应该是
{0,1,2,3,4},
而且我们已经算出
P(X=3)=C43×(43)3×41=6427,
用类似的办法可知
P(X=0)=C40×(43)0×(41)4=2561,
P(X=1)=C41×43×(41)3=643,
P(X=2)=______,
P(X=4)=______,
因此X的分布列为
|X|0|1|2|3|4|
|P|2561|643|______|6427|______|
一般地,如果一次伯努利试验中,出现“成功”的概率为p,记q = 1 - p,且n次独立重复试验中出现“成功”的次数为X,则X的取值范围是
{0,1,…,k,…,n},
而且
P(X=k)=Cnkpkqn−k,k=0,1,…,n,
因此X的分布列如下表所示.
|X|0|1|…|k|…|n|
|P|Cn0p0qn|Cn1p1qn−1|…|Cnkpkqn−k|…|Cnnpnq0|
注意到上述X的分布列第二行中的概率值都是(q+p)n的展开式Cn0p0qn+Cn1p1qn−1+…+Cnkpkqn−k+…+Cnnpnq0中对应项的值,因此称X服从参数为n,p的二项分布,记作
X~B(n,p).
由此可以看出,上述尝试与发现中的随机变量X服从参数为4,43的二项分布,即X~B(4,43). 服从二项分布的随机变量,其概率分布也可用图直观地表示,如图4 - 2 - 4所示.

例1 设本节一开始的情境与问题中,能正常工作的设备数为X.
(1)写出X的分布列;
(2)求出计算机网络不会断掉的概率.
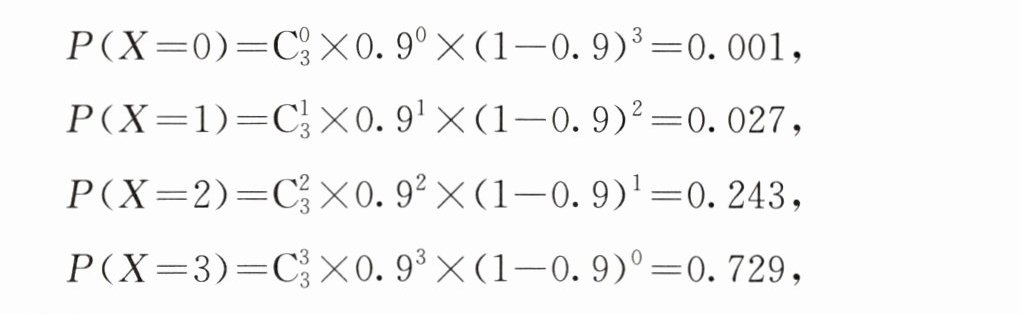
从而X的分布列为

 例2 假设某种人寿保险规定,投保人没活过65岁时,保险公司要赔偿100万元;活过65岁时,保险公司不赔偿. 已知购买此种人寿保险的每个投保人能活过65岁的概率都为0.8. 随机抽取3个投保人,设其中活过65岁的人数为X,保险公司要赔偿给这三人的总金额为Y万元.
例2 假设某种人寿保险规定,投保人没活过65岁时,保险公司要赔偿100万元;活过65岁时,保险公司不赔偿. 已知购买此种人寿保险的每个投保人能活过65岁的概率都为0.8. 随机抽取3个投保人,设其中活过65岁的人数为X,保险公司要赔偿给这三人的总金额为Y万元.
(1)指出X服从的分布;
(2)写出Y与X的关系;
(3)求P(Y=300).
(1)不难看出,X服从参数为3,0.8的二项分布,即

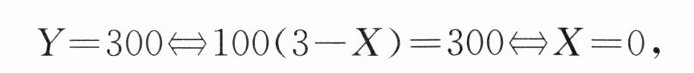

情境与问题
为了增加系统的可靠性,人们经常使用“备用冗余设备”(即正在使用的设备出故障时才启动的设备). 已知某计算机网络的服务器采用的是“一用两备”(即一台正常设备,两台备用设备)的配置,这三台设备中,只要有一台能正常工作,计算机网络就不会断掉. 如果三台设备各自能正常工作的概率都为0.9,它们之间相互不影响,那么这个计算机网络不会断掉的概率是多少呢?
情境中的问题,利用本节所要学习的知识,可以快速地得到解决.
1. n次独立重复试验与二项分布
我们已经知道,一个伯努利试验是试验结果可记为“成功”与“不成功”的试验. 现实生活中,经常需要在相同的条件下将一个伯努利试验重复多次. 例如,为了了解抛硬币时出现的统计规律,可多次重复进行抛硬币这个伯努利试验;为了了解支持改革的人的比例,可随机向多人进行访问,询问他们的态度是“支持”还是“不支持”;等等. 在相同条件下重复n次伯努利试验时,人们总是约定这n次试验是相互独立的,此时这n次伯努利试验也常称为n次独立重复试验.
例如,对一批产品进行抽样检查,每次取一件来判断是否合格,有放回地抽取5次,就是一个5次独立重复试验;篮球运动员练习投篮10次,可以认为每次投中的概率都相同,这是一个10次独立重复试验.
在n次独立重复试验中,人们经常关心的是“成功”出现的次数.
尝试与发现
已知某种药物对某种疾病的治愈率为43,现有甲、乙、丙、丁4个患有该病的患者服用了这种药物,观察其中有多少患者会被这种药物治愈.
(1)这能否看成独立重复试验?
(2)求出甲、乙、丙都被治愈而丁没被治愈的概率;
(3)求出恰有3个患者被治愈的概率;
(4)设有X人被治愈,求X的分布列.
不难想到,4个患者是否会被治愈是相互独立的,因此尝试与发现中的情形可以看成4次独立重复试验.
如果用A1,A2,A3,A4分别表示甲被治愈、乙被治愈、丙被治愈、丁被治愈,则不难看出
P(Ai)=43,P(Ai)=1−P(Ai)=41,i=1,2,3,4.
此时,甲、乙、丙都被治愈而丁没被治愈可以表示为A1A2A3A4,因此由独立性可知
P(A1A2A3A4)=P(A1)P(A2)P(A3)P(A4)
=43×43×43×41=25627.
注意到恰有3个患者被治愈的情况共有C43种(4个人中,选出3个是被治愈的,剩下的那个是没被治愈的),即
A1A2A3A4,A1A2A3A4,A1A2A3A4,A1A2A3A4,
这四种情况两两都是互斥的,而且每一种情况的概率均为(43)3×41=25627,因此所求概率为
P(A1A2A3A4+A1A2A3A4+A1A2A3A4+A1A2A3A4)
=P(A1A2A3A4)+P(A1A2A3A4)+P(A1A2A3A4)+P(A1A2A3A4)
=C43×(43)3×41=6427.
因为共有4名患者服用了药物,所以X的取值范围应该是
{0,1,2,3,4},
而且我们已经算出
P(X=3)=C43×(43)3×41=6427,
用类似的办法可知
P(X=0)=C40×(43)0×(41)4=2561,
P(X=1)=C41×43×(41)3=643,
P(X=2)=______,
P(X=4)=______,
因此X的分布列为
|X|0|1|2|3|4|
|P|2561|643|______|6427|______|
一般地,如果一次伯努利试验中,出现“成功”的概率为p,记q = 1 - p,且n次独立重复试验中出现“成功”的次数为X,则X的取值范围是
{0,1,…,k,…,n},
而且
P(X=k)=Cnkpkqn−k,k=0,1,…,n,
因此X的分布列如下表所示.
|X|0|1|…|k|…|n|
|P|Cn0p0qn|Cn1p1qn−1|…|Cnkpkqn−k|…|Cnnpnq0|
注意到上述X的分布列第二行中的概率值都是(q+p)n的展开式Cn0p0qn+Cn1p1qn−1+…+Cnkpkqn−k+…+Cnnpnq0中对应项的值,因此称X服从参数为n,p的二项分布,记作
X~B(n,p).
由此可以看出,上述尝试与发现中的随机变量X服从参数为4,43的二项分布,即X~B(4,43). 服从二项分布的随机变量,其概率分布也可用图直观地表示,如图4 - 2 - 4所示.

例1 设本节一开始的情境与问题中,能正常工作的设备数为X.
(1)写出X的分布列;
(2)求出计算机网络不会断掉的概率.
解
(1)可以看出,X服从参数为3,0.9的二项分布,即
X~B(3,0.9).
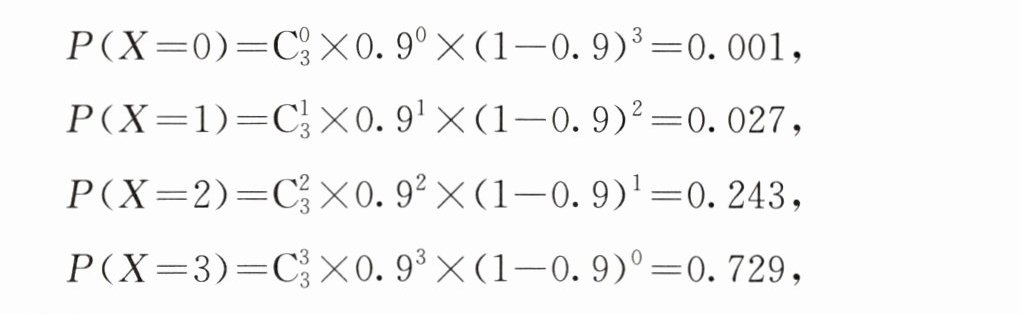
从而X的分布列为

(2)要使得计算机网络不会断掉,也就是要求能正常工作的设备至少
有一台,即 ,因此所求概率为
,因此所求概率为
 ,因此所求概率为
,因此所求概率为
(1)指出X服从的分布;
(2)写出Y与X的关系;
(3)求P(Y=300).
(1)不难看出,X服从参数为3,0.8的二项分布,即

(2)因为3个投保人中,活过65岁的人数为X,则没活过65岁的人
数为3一X,因此
Y=100(3-X).
(3)因为
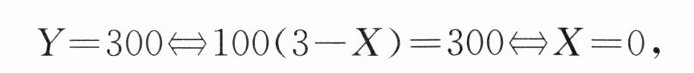
所以

答案:
查看更多完整答案,请扫码查看


