2025年教材课本高中数学选择性必修第二册人教B版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年教材课本高中数学选择性必修第二册人教B版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第24页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
习题3 - 1A
1. 有不同的红球8个,不同的白球7个:
(1)从中取出1个球,共有多少种不同的取法?
(2)从中取出2个颜色不同的球,共有多少种不同的取法?
2. 求下列各式中的正整数$n$:
(1)$\mathrm{A}_{2n}^{3}=10\mathrm{A}_{n}^{3}$; (2)$\mathrm{A}_{10}^{n}=10\times9\times8\times7\times6\times5$。
3. 已知从$n$个不同对象中取出2个对象的排列数等于从$n - 4$个不同对象中取出2个对象的排列数的7倍,求正整数$n$的值。
4. 一部影片在4个单位轮流放映,每一个单位放映一场,共有多少种不同的放映次序?
5. (1)已知圆上有10个点,过任意3个点都可画一个圆内接三角形,一共可画多少个圆内接三角形?
(2)已知空间中有10个点,且任意4个点都不共面,即以任意4个点为顶点都可构造一个四面体,则一共可以构造多少个四面体?
6. (1)平面内有两组平行线,一组有$m$条,另一组有$n$条,不同组的平行线都相交,其中$m$,$n$都是大于1的正整数,这些平行线一共构成了多少个平行四边形?
(2)空间中有三组平行平面,第一组有$m$个,第二组有$n$个,第三组有$l$个,不同组的平面都互相垂直,其中$m$,$n$,$l$都是大于1的正整数,这些平行平面一共构成了多少个长方体?
7. 将4封不同的信全部投入3个邮筒:
(1)不加任何限制,有多少种不同的投法?
(2)每个邮筒至少投1封信,有多少种不同的投法?
8. 某乒乓球邀请赛,参加的有三个组,第一组、第二组各有7个队,第三组有6个队,首先各组进行单循环赛,然后三个组的第一名分主客场进行决赛,最终决出冠、亚军,该乒乓球邀请赛一共需要比赛多少场?
1. 有不同的红球8个,不同的白球7个:
(1)从中取出1个球,共有多少种不同的取法?
(2)从中取出2个颜色不同的球,共有多少种不同的取法?
2. 求下列各式中的正整数$n$:
(1)$\mathrm{A}_{2n}^{3}=10\mathrm{A}_{n}^{3}$; (2)$\mathrm{A}_{10}^{n}=10\times9\times8\times7\times6\times5$。
3. 已知从$n$个不同对象中取出2个对象的排列数等于从$n - 4$个不同对象中取出2个对象的排列数的7倍,求正整数$n$的值。
4. 一部影片在4个单位轮流放映,每一个单位放映一场,共有多少种不同的放映次序?
5. (1)已知圆上有10个点,过任意3个点都可画一个圆内接三角形,一共可画多少个圆内接三角形?
(2)已知空间中有10个点,且任意4个点都不共面,即以任意4个点为顶点都可构造一个四面体,则一共可以构造多少个四面体?
6. (1)平面内有两组平行线,一组有$m$条,另一组有$n$条,不同组的平行线都相交,其中$m$,$n$都是大于1的正整数,这些平行线一共构成了多少个平行四边形?
(2)空间中有三组平行平面,第一组有$m$个,第二组有$n$个,第三组有$l$个,不同组的平面都互相垂直,其中$m$,$n$,$l$都是大于1的正整数,这些平行平面一共构成了多少个长方体?
7. 将4封不同的信全部投入3个邮筒:
(1)不加任何限制,有多少种不同的投法?
(2)每个邮筒至少投1封信,有多少种不同的投法?
8. 某乒乓球邀请赛,参加的有三个组,第一组、第二组各有7个队,第三组有6个队,首先各组进行单循环赛,然后三个组的第一名分主客场进行决赛,最终决出冠、亚军,该乒乓球邀请赛一共需要比赛多少场?
答案:
习题3 - 1B
1. 某教师上午要给3个班上课,每班1节。如果每个班上午只能排4节课,并且该教师不能连上3节课,那么该教师上午的课表有多少种不同的排法?
2. 在不小于3000且不大于7000的正整数中,有多少个没有重复数字的5的倍数?
3. 有6个人分成两排就座,每排3人:
(1)共有多少种不同的坐法?
(2)如果甲不能坐在第一排,乙不能坐在第二排,共有多少种不同的坐法?
(3)如果甲和乙必须在同一排且相邻,共有多少种不同的坐法?
(4)如果甲和乙必须在同一排且不相邻,共有多少种不同的坐法?
4. 某班有35名学生,其中正、副班长各1名,现要从该班选派5名学生参加某种活动:
(1)如果正、副班长必须在内,共有多少种不同的选派方法?
(2)如果正、副班长必须有一人在内,且只能有一人在内,共有多少种不同的选派方法?
(3)如果正、副班长都不在内,共有多少种不同的选派方法?
(4)如果正、副班长至少有一人在内,共有多少种不同的选派方法?
5. 有6个座位连成一排,安排3个人就座,恰有两个空位相邻的不同坐法共有多少种?
6. 有10个人围着一张圆桌坐成一圈,共有多少种不同的坐法?
习题3 - 1C
1. 求$\mathrm{C}_{2}^{2}+\mathrm{C}_{3}^{2}+\mathrm{C}_{4}^{2}+\cdots+\mathrm{C}_{100}^{2}$的值。
2. 求证:$\mathrm{A}_{m}^{m}+\mathrm{A}_{m + 1}^{m}+\mathrm{A}_{m + 2}^{m}+\cdots+\mathrm{A}_{2m}^{m}=\mathrm{A}_{2m + 1}^{m + 1}$。(提示:考察排列数与组合数的关系。)
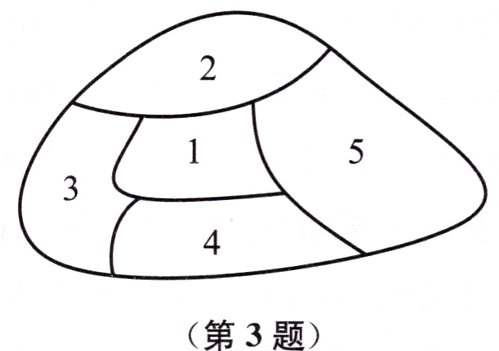
3. 如图所示,一个地区分为5个行政区域,现给地图着色,要求相邻区域不得使用同一颜色,有4种颜色可供选择,则不同的着色方法共有多少种?
4. 要把9本不同的课外书分别装到三个相同的手提袋里,每个袋中至少一本,一共有多少种不同的装法?
5. 把分别标有1号、2号、3号、4号的4个不同的小球放入分别标有1号、2号、3号的3个盒子中,不许有空盒子且任意一个小球都不能放入标有相同标号的盒子中,则不同的放法共有多少种?
1. 某教师上午要给3个班上课,每班1节。如果每个班上午只能排4节课,并且该教师不能连上3节课,那么该教师上午的课表有多少种不同的排法?
2. 在不小于3000且不大于7000的正整数中,有多少个没有重复数字的5的倍数?
3. 有6个人分成两排就座,每排3人:
(1)共有多少种不同的坐法?
(2)如果甲不能坐在第一排,乙不能坐在第二排,共有多少种不同的坐法?
(3)如果甲和乙必须在同一排且相邻,共有多少种不同的坐法?
(4)如果甲和乙必须在同一排且不相邻,共有多少种不同的坐法?
4. 某班有35名学生,其中正、副班长各1名,现要从该班选派5名学生参加某种活动:
(1)如果正、副班长必须在内,共有多少种不同的选派方法?
(2)如果正、副班长必须有一人在内,且只能有一人在内,共有多少种不同的选派方法?
(3)如果正、副班长都不在内,共有多少种不同的选派方法?
(4)如果正、副班长至少有一人在内,共有多少种不同的选派方法?
5. 有6个座位连成一排,安排3个人就座,恰有两个空位相邻的不同坐法共有多少种?
6. 有10个人围着一张圆桌坐成一圈,共有多少种不同的坐法?
习题3 - 1C
1. 求$\mathrm{C}_{2}^{2}+\mathrm{C}_{3}^{2}+\mathrm{C}_{4}^{2}+\cdots+\mathrm{C}_{100}^{2}$的值。
2. 求证:$\mathrm{A}_{m}^{m}+\mathrm{A}_{m + 1}^{m}+\mathrm{A}_{m + 2}^{m}+\cdots+\mathrm{A}_{2m}^{m}=\mathrm{A}_{2m + 1}^{m + 1}$。(提示:考察排列数与组合数的关系。)
3. 如图所示,一个地区分为5个行政区域,现给地图着色,要求相邻区域不得使用同一颜色,有4种颜色可供选择,则不同的着色方法共有多少种?

4. 要把9本不同的课外书分别装到三个相同的手提袋里,每个袋中至少一本,一共有多少种不同的装法?
5. 把分别标有1号、2号、3号、4号的4个不同的小球放入分别标有1号、2号、3号的3个盒子中,不许有空盒子且任意一个小球都不能放入标有相同标号的盒子中,则不同的放法共有多少种?
答案:
查看更多完整答案,请扫码查看


