2025年全优少年课时训练五年级数学下册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年全优少年课时训练五年级数学下册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第33页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
1. 先把一个正方体的表面涂上颜色,再把这个正方体的棱长等分成2份、3份、4份……最后切成小正方体。不管棱长等分成多少份,三面涂色的小正方体都只有( )块。
答案:
8 [提示]不管棱长等分成多少份,三面涂色的小正方体始终在原来正方体的顶点上,正方体有8个顶点,所以三面涂色的小正方体只有8个。
8 [提示]不管棱长等分成多少份,三面涂色的小正方体始终在原来正方体的顶点上,正方体有8个顶点,所以三面涂色的小正方体只有8个。

$2. $选一选。
$(1)9$个小正方体拼成的几何体如下图所示,如果把它的表面涂色,那么三面涂色的小正方体有$( )$个。
$A. 1 B. 2 C. 3 D. 4$
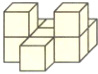
$(2)$用$27$个小正方体拼成的几何体如下图所示,若将其表面涂色,则三面涂色的小正方体有$( )$个。
$A. 7 B. 8 C. 9 D. 10$

$(1)9$个小正方体拼成的几何体如下图所示,如果把它的表面涂色,那么三面涂色的小正方体有$( )$个。
$A. 1 B. 2 C. 3 D. 4$

$(2)$用$27$个小正方体拼成的几何体如下图所示,若将其表面涂色,则三面涂色的小正方体有$( )$个。
$A. 7 B. 8 C. 9 D. 10$

答案:
(1)C
(2)C
(1)C
(2)C
$3. ($几何直观$)$摆一摆,填一填。
$(1)$右面的立体图形一共有$( )$层。
$(2)$数一数每层$($从上往下$)$有几个小正方体,把表格填完整。
 $ $
$ $

$(3)$你发现了什么规律$?$
$(4)$照这样的规律,第$10$层、第$100$层分别有多少块小正方体$?$
$(1)$右面的立体图形一共有$( )$层。
$(2)$数一数每层$($从上往下$)$有几个小正方体,把表格填完整。
 $ $
$ $
$(3)$你发现了什么规律$?$
$(4)$照这样的规律,第$10$层、第$100$层分别有多少块小正方体$?$
答案:
(1)6
(2)1 4 9 16 25 36
(3)层数的平方就是每层小正方体的块数。
(4)100块 10000块
(1)6
(2)1 4 9 16 25 36
(3)层数的平方就是每层小正方体的块数。
(4)100块 10000块
4. (直观想象)想一想,填一填,算一算。
(1)右图中正方体的表面涂满了红色,然后切开。切开的小正方体中,三面涂红色的有( )块,两面涂红色的有( )块,一面涂红色的有( )块,没有涂色的有( )块。
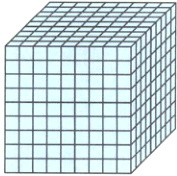
(2)先把1 m³的正方体木块的表面涂上颜色,再切成若干个1 dm³的小正方体,在这些小正方体中,一面涂色的小正方体共有多少块?
(1)右图中正方体的表面涂满了红色,然后切开。切开的小正方体中,三面涂红色的有( )块,两面涂红色的有( )块,一面涂红色的有( )块,没有涂色的有( )块。

(2)先把1 m³的正方体木块的表面涂上颜色,再切成若干个1 dm³的小正方体,在这些小正方体中,一面涂色的小正方体共有多少块?
答案:
(1)8 84 294 343
(2)$6×(10 - 2)×(10 - 2)=384$(块)
(1)8 84 294 343
(2)$6×(10 - 2)×(10 - 2)=384$(块)
查看更多完整答案,请扫码查看


