《2025年赢在假期期末加寒假七年级数学沪科版合肥工业大学出版社》

11. 有甲、乙两种商品，若购甲2件、乙1件共需120元，若购甲1件、乙2件共需180元，则购甲、乙两种商品各1件共需_______元.

答案： 100

12. 材料：如果一个四位自然数$M$的十位数字等于千位数字的两倍，百位数学与个位数字的差为3，且各个数位的数字均不为0，把它的前两位数字组成的两位数记为$x$，后两位数字组成的两位数记为$y$，规定$F(M)=2x + y$，当$F(M)$能被7整除时，称这个四位数为“奇妙数”. 若“奇妙数”$M=\overline{abcd}$（$1\leqslant a,b,c,d\leqslant9$，$a$，$b$，$c$，$d$为整数），则$F(M)=$_______（用含字母$a$和$d$的代数式表示），符合条件的“奇妙数”$M$的最大值与最小值的差为_______.

答案： $40a + 3d + 6$ 3262

13. 用合适的方法解方程组.

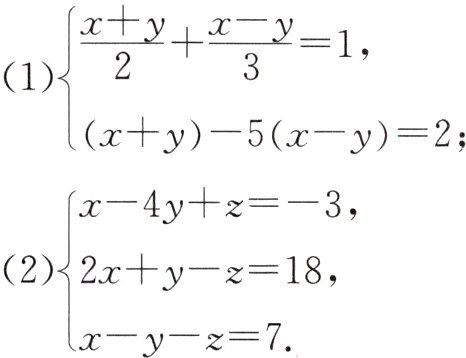
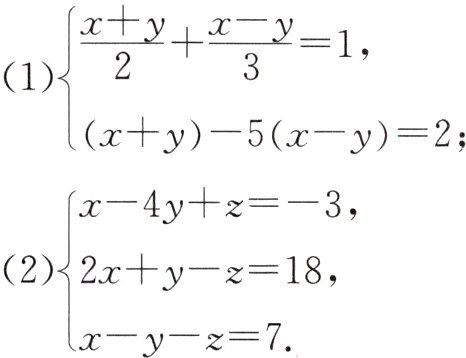
答案： 解：
(1)设$x + y = a$，$x - y = b$，则原方程组变成$\begin{cases}\frac{1}{2}a + \frac{1}{3}b = 1\\a - 5b = 2\end{cases}$，解得$\begin{cases}a = 2\\b = 0\end{cases}$，把$\begin{cases}a = 2\\b = 0\end{cases}$代入$x + y = a$，$x - y = b$，得$\begin{cases}x + y = 2\\x - y = 0\end{cases}$，解得$\begin{cases}x = 1\\y = 1\end{cases}$，所以原方程组的解为$\begin{cases}x = 1\\y = 1\end{cases}$；
(2)$\begin{cases}x - 4y + z = -3①\\2x + y - z = 18②\\x - y - z = 7③\end{cases}$，由① + ②，得$3x - 3y = 15$，即$x - y = 5$④，把④代入③式，可得出$z = -2$，把$z = -2$代入①，②得$\begin{cases}x - 4y = -1\\2x + y = 16\end{cases}$，解得$\begin{cases}x = 7\\y = 2\end{cases}$，所以原方程组的解为$\begin{cases}x = 7\\y = 2\\z = -2\end{cases}$。

14. 已知关于$x$，$y$的方程组$\begin{cases}x + 2y - 6 = 0\\x - 2y + mx + 4m = 0\end{cases}$.
(1) 若方程组的解满足$x + y = 0$，求$m$的值；
(2) 无论实数$m$取何值，方程$x - 2y + mx + 4m = 0$总有一个固定的解，请求出这个解；
(3) 若方程组的解中$x$为整数，且$m$是自然数，求$m$的值.

答案： 解：
(1)由题意得$\begin{cases}x + y = 0\\x + 2y - 6 = 0\end{cases}$，解得$\begin{cases}x = -6\\y = 6\end{cases}$，把$\begin{cases}x = -6\\y = 6\end{cases}$代入$x - 2y + mx + 4m = 0$，解得$m = -9$；
(2)$x - 2y + mx + 4m = 0$，$x - 2y + m(x + 4) = 0$，所以当$x + 4 = 0$，$x = -4$时，$y = -2$，即固定的解为$\begin{cases}x = -4\\y = -2\end{cases}$；
(3)$\begin{cases}x + 2y - 6 = 0①\\x - 2y + mx + 4m = 0②\end{cases}$，① + ②得$2x - 6 + mx + 4m = 0$，$(2 + m)x = 6 - 4m$，$x = \frac{6 - 4m}{m + 2} = \frac{-4(m + 2) + 14}{m + 2} = -4 + \frac{14}{m + 2}$。因为$x$为整数，所以$m + 2 = \pm1,\pm2,\pm7,\pm14$，且$m$为自然数，所以$m + 2 = 2$或$7$或$14$，$m = 0$或$5$或$12$。

15. 一家工厂里2个男工和4个女工一天可加工全部零件的$\frac{3}{10}$，8个男工和10个女工一天内可加工完全部零件. 如果把单独让男工加工和单独让女工加工进行比较，要在一天内完成任务，女工要比男工多多少人？

答案： 解：设男工的工作效率为$x$，女工的工作效率为$y$，根据题意得$\begin{cases}2x + 4y = \frac{3}{10}\\8x + 10y = 1\end{cases}$，解得$\begin{cases}x = \frac{1}{12}\\y = \frac{1}{30}\end{cases}$，如果单独让男工加工或单独让女工加工，需要男工$1\div\frac{1}{12} = 12$（人），需要女工$1\div\frac{1}{30} = 30$（人），女工比男工多$30 - 12 = 18$（人）。故女工比男工要多18人。

16. 某汽车销售公司计划购进一批新能源汽车尝试进行销售，据了解2辆$A$型汽车、3辆$B$型汽车的进价共计80万元；3辆$A$型汽车、2辆$B$型汽车的进价共计95万元.
(1) 求$A$、$B$两种型号的汽车每辆进价分别为多少万元？
(2) 若该公司计划正好用180万元购进以上两种型号的新能源汽车（两种型号的汽车均购买），请你帮助该公司设计购买方案；
(3) 若该汽车销售公司销售1辆$A$型汽车可获利8000元，销售1辆$B$型汽车可获利6000元，在(2)中的购买方案中，假如这些新能源汽车全部售出，哪种方案获利最大？最大利润是多少元？

答案： 解：
(1)设$A$种型号的汽车每辆进价为$a$万元，$B$种型号的汽车每辆进价为$b$万元，由题意可得$\begin{cases}2a + 3b = 80\\3a + 2b = 95\end{cases}$，解得$\begin{cases}a = 25\\b = 10\end{cases}$，答：$A$、$B$两种型号的汽车每辆进价分别为25万元、10万元。
(2)设购买$A$型号的汽车$m$辆，$B$型号的汽车$n$辆，由题意可得$25m + 10n = 180$且$m＞0$，$n＞0$，解得$\begin{cases}m = 2\\n = 13\end{cases}$或$\begin{cases}m = 4\\n = 8\end{cases}$或$\begin{cases}m = 6\\n = 3\end{cases}$，所以该公司共有三种购买方案：方案一：购买2辆$A$型汽车，购买13辆$B$型汽车；方案二：购买4辆$A$型汽车，购买8辆$B$型汽车；方案三：购买6辆$A$型汽车，购买3辆$B$型汽车；
(3)当$m = 2$，$n = 13$时，获得的利润为$8000\times2 + 6000\times13 = 94000$（元）；当$m = 4$，$n = 8$时，获得的利润为$8000\times4 + 6000\times8 = 80000$（元）；当$m = 6$，$n = 3$时，获得的利润为$8000\times6 + 6000\times3 = 66000$（元）；由上可得，最大利润为94000元。所以购买2辆$A$型汽车，购买13辆$B$型汽车获利最大，最大利润为94000元。