2025年赢在假期期末加寒假七年级数学沪科版合肥工业大学出版社
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年赢在假期期末加寒假七年级数学沪科版合肥工业大学出版社 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
7. 下列说法:①无限小数都是无理数;②无理数都是无限小数;③带根号的数都是无理数;④$0.\dot{3}\dot{2}$是无理数。其中错误的是________。(填序号)
答案:
①③④
8. 有一个数值转换器,原理如图所示,当输入的$x$的值为64时,输出的$y$的值是________。


答案:
$\sqrt{8}$
9. 把下列各数填在相应的大括号内:
$0$,$−2$,$\sqrt{3}$,$−\sqrt{27}$,$0.1^{2}$,$−\sqrt[3]{\frac{8}{27}}$,$\sqrt{4}$,$\frac{22}{7}$,$\frac{\sqrt{3}}{2}$,$1.\dot{2}\dot{1}$,$0.1010010001\cdots$(两个1之间依次增加一个0),$\frac{\pi}{4}$。
有理数:{ ,…};
无理数:{ ,…};
非负数:{ ,…};
分数:{ ,…};
负实数:{ ,…}。
$0$,$−2$,$\sqrt{3}$,$−\sqrt{27}$,$0.1^{2}$,$−\sqrt[3]{\frac{8}{27}}$,$\sqrt{4}$,$\frac{22}{7}$,$\frac{\sqrt{3}}{2}$,$1.\dot{2}\dot{1}$,$0.1010010001\cdots$(两个1之间依次增加一个0),$\frac{\pi}{4}$。
有理数:{ ,…};
无理数:{ ,…};
非负数:{ ,…};
分数:{ ,…};
负实数:{ ,…}。
答案:
有理数:$\{0, -2, 0.1^{2}, -\sqrt[3]{\frac{8}{27}}, \sqrt{4}, \frac{22}{7}, 1.\dot{2}\dot{1}\cdots\}$ 无理数:$\{\sqrt{3}, -\sqrt{27}, \frac{\sqrt{3}}{2}, 0.1010010001\cdots$(两个 1 之间依次增加一个 0)$, \frac{\pi}{4}\cdots\}$ 非负数:$\{0, \sqrt{3}, 0.1^{2}, \sqrt{4}, \frac{22}{7}, \frac{\sqrt{3}}{2}, 1.\dot{2}\dot{1}, 0.1010010001\cdots$(两个 1 之间依次增加一个 0)$, \frac{\pi}{4}, \cdots\}$ 分数:$\{0.1^{2}, -\sqrt[3]{\frac{8}{27}}, \frac{22}{7}, 1.\dot{2}\dot{1}, \cdots\}$ 负实数:$\{-2, -\sqrt{27}, -\sqrt[3]{\frac{8}{27}}, \cdots\}$
10. 已知$\sqrt{2x - y^{3}}+\vert y^{3}-8\vert = 0$,试判断$\sqrt[3]{x}$是有理数还是无理数?
答案:
解:因为$\sqrt{2x - y^{3}} + |y^{3} - 8| = 0$,所以$\sqrt{2x - y^{3}} = 0$,$|y^{3} - 8| = 0$,所以$2x - y^{3} = 0$,$y^{3} - 8 = 0$,所以$y^{3} = 2x$,$y^{3} = 8$,所以$y = 2$,$x = 4$,所以$\sqrt[3]{x} = \sqrt[3]{4} = 2$,所以$\sqrt[3]{x}$是有理数.
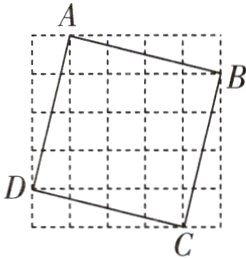
11. 如图所示,四边形$ABCD$是$5×5$网格中的格点正方形,网格中的每个小正方形的边长均为1。
(1)求正方形$ABCD$的面积;
(2)判断正方形$ABCD$的边长是有理数还是无理数。
(1)求正方形$ABCD$的面积;
(2)判断正方形$ABCD$的边长是有理数还是无理数。

答案:
解:
(1) 正方形$ABCD$的面积$= 5^{2} - 4\times\frac{1}{2}\times1\times4 = 17$;
(2) 设正方形$ABCD$的边长为$x$,则$x^{2} = 17$,解得$x = \sqrt{17}$(负值舍去),它是无理数.
(1) 正方形$ABCD$的面积$= 5^{2} - 4\times\frac{1}{2}\times1\times4 = 17$;
(2) 设正方形$ABCD$的边长为$x$,则$x^{2} = 17$,解得$x = \sqrt{17}$(负值舍去),它是无理数.
12. 现有四个实数$a$,$b$,$c$,$d$,其中$a$是开立方运算中结果最小的正整数,$b$是开平方运算中结果唯一的数,$c$是9的立方根,$d$是36的算术平方根。
(1)直接写出$a$,$b$,$c$,$d$的值;
(2)从$a$,$b$,$c$,$d$中任取两个数(不重复选取)组成一个两位数,求这个两位数的算术平方根,并说明所得结果是有理数还是无理数。
(1)直接写出$a$,$b$,$c$,$d$的值;
(2)从$a$,$b$,$c$,$d$中任取两个数(不重复选取)组成一个两位数,求这个两位数的算术平方根,并说明所得结果是有理数还是无理数。
答案:
解:
(1) 因为$a$是开立方运算中结果最小的正整数,所以$a = 1$. 因为$b$是开平方运算中结果唯一的数,所以$b = 0$. 因为$c$是 9 的立方根,所以$c = \sqrt[3]{9}$. 因为$d$是 36 的算术平方根,所以$d = \sqrt{36} = 6$;
(2) 因为$c = \sqrt[3]{9}$是一个无理数,所以从$a, b, c, d$中任取两个数(不重复选取)组成一个两位数为 10, 16, 60, 61. 这几个两位数的算术平方根分别为:$\sqrt{10}$,$\sqrt{16} = 4$,$\sqrt{60} = 2\sqrt{15}$,$\sqrt{61}$,其中,$\sqrt{10}$,$2\sqrt{15}$,$\sqrt{61}$是无理数,4 是有理数.
(1) 因为$a$是开立方运算中结果最小的正整数,所以$a = 1$. 因为$b$是开平方运算中结果唯一的数,所以$b = 0$. 因为$c$是 9 的立方根,所以$c = \sqrt[3]{9}$. 因为$d$是 36 的算术平方根,所以$d = \sqrt{36} = 6$;
(2) 因为$c = \sqrt[3]{9}$是一个无理数,所以从$a, b, c, d$中任取两个数(不重复选取)组成一个两位数为 10, 16, 60, 61. 这几个两位数的算术平方根分别为:$\sqrt{10}$,$\sqrt{16} = 4$,$\sqrt{60} = 2\sqrt{15}$,$\sqrt{61}$,其中,$\sqrt{10}$,$2\sqrt{15}$,$\sqrt{61}$是无理数,4 是有理数.
查看更多完整答案,请扫码查看


