《2025年赢在假期期末加寒假七年级数学沪科版合肥工业大学出版社》

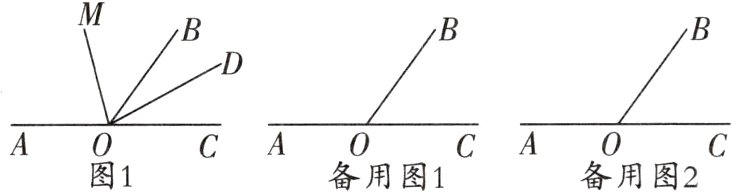
针对训练2　如图1,点A,O,C在同一条直线上,∠AOB=126°,射线OD在直线AC的上方绕点O旋转，记∠COD = α,OM平分∠AOD.
(1)若∠AOD与∠BOD互补,则∠α =____；
(2)若∠BOD=90°,则∠MOB=________;
(3)是否存在α的值,使得∠MOD与∠BOD 互余,若存在,求出α,若不存在,请说明理由.

答案：
针对训练2.解:
(1)因为点A,O,C在同一条直线上，所以∠AOC=180°,所以∠BOC=180°−∠AOB=180°−126°=54°,所以∠BOD=∠BOC−∠COD=54°−α,所以∠AOD+∠BOD=∠AOB+2∠BOD=126°+2(54°−α)=180°,解得α=27°,故答案为:27°;
(2)如图1
因为点A,O,C在同一条直线上，所以∠AOC=180°,所以∠BOC=180°−∠AOB=180°−126°=54°,所以∠BOD=∠COD−∠BOC=α−54°=90°,即α=144°,所以∠AOD=180°−α=180°−144°=36°.因为OM平分∠AOD,所以∠MOD=∠AOM=$\frac{1}{2}$∠AOD=$\frac{1}{2}$×36°=18°,所以∠MOB=∠MOD+∠BOD=18°+90°=108°,故答案为:108°;
(3)存在,因为∠MOD与∠BOD互余,所以∠MOD+∠BOD=90°.因为∠COD=α,OM平分∠AOD,所以∠MOD=$\frac{1}{2}$(180°−α),
①如图2,
因为∠BOD =180°−126°−α,所以$\frac{1}{2}$(180°−α)+180°−126°−α=90°,解得α=36°;
②如图3,
　　　　　　　　　　　　
∠BOD=∠AOB−∠AOD=126°−(180°−α)=α−54°,所以$\frac{1}{2}$(180°−α)+α−54°=90°,解得α=108°,
综上所述，α的值为36°或108°.

经典例题3　(江苏无锡.中考)如图,已知∠AOC=90°,∠COB=α,OD平分∠AOB.
(1)用含α的式子表示∠COD的度数;
(2)若α=50°,求∠COD的度数.

解析　(1)因为∠AOC=90°,∠COB=α,所以∠AOB=∠AOC+∠COB=90°+α.因为OD平分∠AOB,所以∠AOD=$\frac{1}{2}$∠AOB =45°+$\frac{1}{2}$α,所以∠COD=∠AOC−∠AOD =90°−(45°+$\frac{1}{2}$α)=45°−$\frac{1}{2}$α;(2)因为α=50°,所以∠COD=45°−$\frac{1}{2}$×50°=20°.

答案：

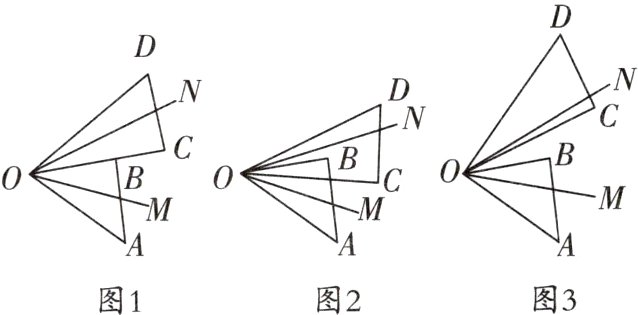
针对训练3　将一副三角板的两个锐角顶点重合，∠AOB=45°,∠COD=30°,OM,ON分别是∠AOC,∠BOD的平分线.
(1)如图1所示,当OB与OC重合时,则∠MON=________;
(2)当∠COD绕着点O旋转至如图2所示，当∠BOC=14°,则∠MON=________;
(3)当∠COD绕着点O旋转至如图3所示，当∠BOC=α时,求∠MON的大小.

答案： 针对训练3.解:
(1)因为∠AOB=45°,∠COD=30°,OM,ON分别是∠AOC,∠COD的平分线，所以∠BOM=$\frac{1}{2}$∠AOB=22.5°,∠CON=$\frac{1}{2}$∠COD=15°,所以∠MON=∠BOM+∠CON=22.5°+15°=37.5°.故答案为:37.5°.
(2)当∠BOC=14°时,∠AOC=45°−14°=31°,∠BOD=30°−14°=16°,因为OM,ON分别是∠AOC,∠BOD的平分线，所以∠BON=$\frac{1}{2}$∠BOD=$\frac{1}{2}$×16°=8°,∠MOC=$\frac{1}{2}$∠AOC=15.5°,所以∠MON=∠MOC+∠BON+∠BOC=15.5°+8°+14°=37.5°;
(3)当∠BOC=α时,∠AOC=45°+α,∠BOD=30°+α,因为OM,ON分别是∠AOC,∠BOD的平分线，所以∠BON=$\frac{1}{2}$∠BOD=$\frac{1}{2}$(30°+α)=15°+$\frac{1}{2}$α,∠MOB =$\frac{1}{2}$∠AOC−∠BOC=$\frac{1}{2}$(45°+α)−α=22.5°−$\frac{1}{2}$α,所以∠MON=∠MOB+∠BON=22.5°−$\frac{1}{2}$α+15°+$\frac{1}{2}$α=37.5°.