2025年赢在假期期末加寒假七年级数学沪科版合肥工业大学出版社
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年赢在假期期末加寒假七年级数学沪科版合肥工业大学出版社 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
8. 下面是一个长方体的四个面,另两个面的面积和是( )

A. 25 cm²
B. 35 cm²
C. 40 cm²
D. 70 cm²

A. 25 cm²
B. 35 cm²
C. 40 cm²
D. 70 cm²
答案:
8.D
9. 一个几何体由若干大小相同的小立方块搭成,如图分别是从它的正面、上面看到的形状图,则搭成这个几何体的小立方块最少需要_______个,最多需要_______个.


答案:
9.6 8
10. 有甲、乙两个底面积相等的圆柱,甲圆柱高6.28厘米,侧面展开是正方形;乙圆柱高3.6厘米,它的体积是________立方厘米.(π取3.14)
答案:
10.11.304
11. 已知A,B,C为同一平面内不共线的三点,点D分线段AC,BC的和为相等的两部分,若AC=10,CD=3,则线段BC长为________.
答案:
11.4或16
12. 如图,B在线段AC上,且BC=3AB,D是线段AB的中点,E是BC的三等分点,则下列结论:①3EC=AE;②DE=3BD;③2BE=AE+BC;④5AE=6(BC-AD),其中正确结论的有_______.(填序号)


答案:
12.①④
13. 如图,已知四点A,B,C,D. 用圆规和无刻度的直尺按要求画出图形:
(1)画直线AB;
(2)画射线DC;
(3)延长线段DA至点E,使AE=AB;(保留作图痕迹)
(4)在AB上找一点P,使PC+PE的值最小,并说明作图依据.
(1)画直线AB;
(2)画射线DC;
(3)延长线段DA至点E,使AE=AB;(保留作图痕迹)
(4)在AB上找一点P,使PC+PE的值最小,并说明作图依据.
答案:
13.解:
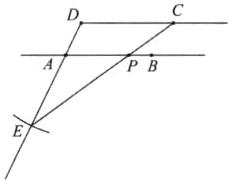
(1)如图,直线AB即为所求作的直线;
(2)如图,射线DC即为所求作的射线;
(3)如图,AE = AB;
(4)连接EC交AB于点P,则PC + PE的值最小,理由是:两点之间线段最短.
13.解:

(1)如图,直线AB即为所求作的直线;
(2)如图,射线DC即为所求作的射线;
(3)如图,AE = AB;
(4)连接EC交AB于点P,则PC + PE的值最小,理由是:两点之间线段最短.
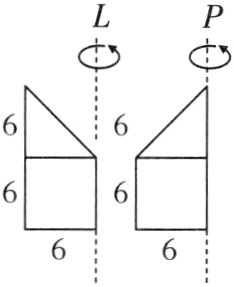
14. 如图,将下面组合图形分别绕轴L、轴P旋转一周形成两个不同的立体图. 请问这两个立体图形体积的比是多少?

答案:
14.解:第一个图形形成的立体图形的体积:π×6²×12 - $\frac{1}{3}$π×6²×6 = 432π - 72π = 360π;第二个图形形成的立体图形的体积:π×6²×6 + $\frac{1}{3}$π×6²×6 = 216π + 72π = 288π.所以两个立体图形体积的比是(360π):(288π)=5:4.
15. 如图,点A,B,C,O是在数轴上的点,其中点O表示的数是0,点A,B,C表示的数分别为a,b,c.
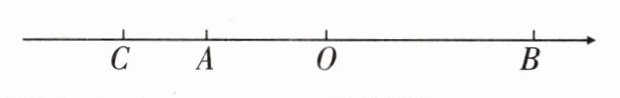
(1)图中共有_______条线段.
(2)若AO:BO=2:3,O为CB的中点,且CA=3,求a,b,c的值.
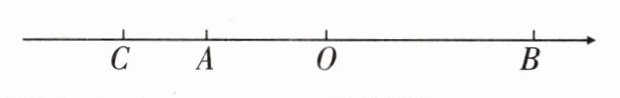
(1)图中共有_______条线段.
(2)若AO:BO=2:3,O为CB的中点,且CA=3,求a,b,c的值.
答案:
15.解:
(1)因为线段有两个端点,所以图中有线段:线段CA、线段CO、线段CB、线段AO、线段AB、线段OB,即图中共有6条线段;
(2)因为AO:BO = 2:3,所以设AO = 2x,BO = 3x.因为O为CB中点,所以OC = OB = 3x.因为CA = 3且CA + AO = OC,所以3 + 2x = 3x,解得x = 3,所以AO = 2x = 2×3 = 6,OC = OB = 3x = 3×3 = 9,所以a = -6,b = 9,c = -9.
(1)因为线段有两个端点,所以图中有线段:线段CA、线段CO、线段CB、线段AO、线段AB、线段OB,即图中共有6条线段;
(2)因为AO:BO = 2:3,所以设AO = 2x,BO = 3x.因为O为CB中点,所以OC = OB = 3x.因为CA = 3且CA + AO = OC,所以3 + 2x = 3x,解得x = 3,所以AO = 2x = 2×3 = 6,OC = OB = 3x = 3×3 = 9,所以a = -6,b = 9,c = -9.
查看更多完整答案,请扫码查看


