2025年赢在假期期末加寒假七年级数学沪科版合肥工业大学出版社
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年赢在假期期末加寒假七年级数学沪科版合肥工业大学出版社 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
三、解答题
12. 观察下列等式:
第①个等式:$3×1×2 = 1×2×3 - 0×1×2$
第②个等式:$3×2×3 = 2×3×4 - 1×2×3$
第③个等式:$3×3×4 = 3×4×5 - 2×3×4$
根据上述规律解决下列问题:
(1)完成第④个等式:________________;
(2)写出你猜想的第$n$个等式(用含$n$的式子表示),并验证其正确性;
(3)根据你发现的规律,可知$1×2 + 2×3 + 3×4 + \cdots + 99×100=$______.(直接写出结果即可)
12. 观察下列等式:
第①个等式:$3×1×2 = 1×2×3 - 0×1×2$
第②个等式:$3×2×3 = 2×3×4 - 1×2×3$
第③个等式:$3×3×4 = 3×4×5 - 2×3×4$
根据上述规律解决下列问题:
(1)完成第④个等式:________________;
(2)写出你猜想的第$n$个等式(用含$n$的式子表示),并验证其正确性;
(3)根据你发现的规律,可知$1×2 + 2×3 + 3×4 + \cdots + 99×100=$______.(直接写出结果即可)
答案:
解:
(1)第④个等式:$3×4×5 = 4×5×6 - 3×4×5$;
(2)第$n$个等式是$3n(n + 1)=n(n + 1)(n + 2)-(n - 1)n(n + 1)$.右边$=(n + 1)(n^{2}+2n - n^{2}+n)=3n(n + 1)=$左边,所以等式成立;
(3)原式$=\frac{1}{3}×(3×1×2 + 3×2×3 + 3×3×4+\cdots+3×99×100)=\frac{1}{3}×(1×2×3 - 0×1×2 + 2×3×4 - 1×2×3 + 3×4×5 - 2×3×4+\cdots+99×100×101 - 98×99×100)=\frac{1}{3}×99×100×101 = 333300$,故答案为333300.
(1)第④个等式:$3×4×5 = 4×5×6 - 3×4×5$;
(2)第$n$个等式是$3n(n + 1)=n(n + 1)(n + 2)-(n - 1)n(n + 1)$.右边$=(n + 1)(n^{2}+2n - n^{2}+n)=3n(n + 1)=$左边,所以等式成立;
(3)原式$=\frac{1}{3}×(3×1×2 + 3×2×3 + 3×3×4+\cdots+3×99×100)=\frac{1}{3}×(1×2×3 - 0×1×2 + 2×3×4 - 1×2×3 + 3×4×5 - 2×3×4+\cdots+99×100×101 - 98×99×100)=\frac{1}{3}×99×100×101 = 333300$,故答案为333300.
13. 已知$A = 3x^{2}-x + 2y - 4xy$,$B = 2x^{2}-3x - y + xy$.
(1)化简:$2A - 3B$;
(2)若$x + y = -\frac{6}{7}$,$xy = 1$,求$2A - 3B$的值;
(3)若$2A - 3B$的值与$y$的取值无关,求此时$2A - 3B$的值.
(1)化简:$2A - 3B$;
(2)若$x + y = -\frac{6}{7}$,$xy = 1$,求$2A - 3B$的值;
(3)若$2A - 3B$的值与$y$的取值无关,求此时$2A - 3B$的值.
答案:
解:
(1)因为$A = 3x^{2}-x + 2y - 4xy$,$B = 2x^{2}-3x - y+xy$,所以$2A - 3B = 2(3x^{2}-x + 2y - 4xy)-3(2x^{2}-3x - y+xy)=6x^{2}-2x + 4y - 8xy - 6x^{2}+9x + 3y - 3xy = 7x + 7y - 11xy$;
(2)因为$x + y = -\frac{6}{7}$,$xy = 1$,所以$2A - 3B = 7x + 7y - 11xy = 7(x + y)-11xy = 7×(-\frac{6}{7})-11×1=-6 - 11=-17$;
(3)由
(1)可知$2A - 3B = 7x+(7 - 11x)y$,因为$2A - 3B$的值与$y$的取值无关,所以$7 - 11x = 0$,所以$x = \frac{7}{11}$,所以$2A - 3B = 7x+(7 - 11x)y = 7×\frac{7}{11}=\frac{49}{11}$.
(1)因为$A = 3x^{2}-x + 2y - 4xy$,$B = 2x^{2}-3x - y+xy$,所以$2A - 3B = 2(3x^{2}-x + 2y - 4xy)-3(2x^{2}-3x - y+xy)=6x^{2}-2x + 4y - 8xy - 6x^{2}+9x + 3y - 3xy = 7x + 7y - 11xy$;
(2)因为$x + y = -\frac{6}{7}$,$xy = 1$,所以$2A - 3B = 7x + 7y - 11xy = 7(x + y)-11xy = 7×(-\frac{6}{7})-11×1=-6 - 11=-17$;
(3)由
(1)可知$2A - 3B = 7x+(7 - 11x)y$,因为$2A - 3B$的值与$y$的取值无关,所以$7 - 11x = 0$,所以$x = \frac{7}{11}$,所以$2A - 3B = 7x+(7 - 11x)y = 7×\frac{7}{11}=\frac{49}{11}$.
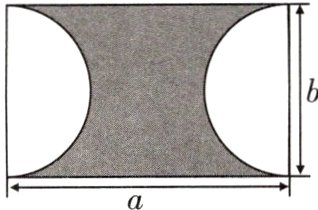
14. 如图,长方形的长为$a$,宽为$b$.
(1)用含$a$,$b$的代数式表示图中阴影部分的面积$S$;
(2)当$a = 4\ cm$,$b = 2\ cm$时,求$S$.($\pi$取3.14)
(1)用含$a$,$b$的代数式表示图中阴影部分的面积$S$;
(2)当$a = 4\ cm$,$b = 2\ cm$时,求$S$.($\pi$取3.14)

答案:
解:
(1)$S = ab-\pi(\frac{b}{2})^{2}=ab-\frac{1}{4}\pi b^{2}$;
(2)当$a = 4\ cm$,$b = 2\ cm$,$\pi$取3.14时,$S = 4×2-\frac{1}{4}×3.14×2^{2}=8 - 3.14 = 4.86\ cm^{2}$.
(1)$S = ab-\pi(\frac{b}{2})^{2}=ab-\frac{1}{4}\pi b^{2}$;
(2)当$a = 4\ cm$,$b = 2\ cm$,$\pi$取3.14时,$S = 4×2-\frac{1}{4}×3.14×2^{2}=8 - 3.14 = 4.86\ cm^{2}$.
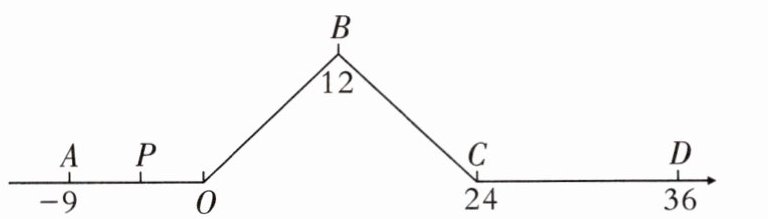
15. 七年级数学兴趣小组成员自主开展数学微项目研究,他们决定研究“折线数轴”. 如图,将一条数轴在原点$O$,点$B$,点$C$处折一下,得到一条“折线数轴”. 图中点$A$表示-9,点$B$表示12,点$C$表示24,点$D$表示36,动点$P$从点$A$出发,以2个单位长度/秒的初始速度沿着“折线数轴”向其正方向运动. 当运动到点$O$与点$B$之间时速度变为初始速度的一半;当运动到点$B$与点$C$之间时速度变为初始速度的2倍;经过点$C$后立刻恢复初始速度.
(1)动点$P$从点$A$运动至点$B$需要______秒;
(2)动点$P$从点$A$出发,运动$t$秒至点$B$和点$C$之间时,则点$P$表示的数______(用含$t$的式子表示).
(1)动点$P$从点$A$运动至点$B$需要______秒;
(2)动点$P$从点$A$出发,运动$t$秒至点$B$和点$C$之间时,则点$P$表示的数______(用含$t$的式子表示).

答案:
解:
(1)因为点$A$表示$-9$,点$B$表示12,所以$OA = 9$,$OB = 12$.因为动点$P$在$AO$段初始速度为2个单位长度/秒,动点$P$在$OB$段速度为初始速度的一半,所以动点$P$在$OB$段速度为1个单位长度/秒,所以动点$P$从点$A$运动至点$B$的时间:$\frac{9}{2}+\frac{12}{1}=\frac{33}{2}$(秒);
(2)因为动点$P$的初始速度为2个单位长度/秒,动点$P$在$BC$段速度为初始速度的两倍,所以$P$在$BC$段速度为4个单位长度/秒,由
(1)可得动点$P$在$BC$段运动时间为$(t - 16.5)$秒,所以$BP = 4(t - 16.5)=4t - 66$.因为点$B$表示12,所以$P$表示的数为$12+(4t - 66)=4t - 54$.
(1)因为点$A$表示$-9$,点$B$表示12,所以$OA = 9$,$OB = 12$.因为动点$P$在$AO$段初始速度为2个单位长度/秒,动点$P$在$OB$段速度为初始速度的一半,所以动点$P$在$OB$段速度为1个单位长度/秒,所以动点$P$从点$A$运动至点$B$的时间:$\frac{9}{2}+\frac{12}{1}=\frac{33}{2}$(秒);
(2)因为动点$P$的初始速度为2个单位长度/秒,动点$P$在$BC$段速度为初始速度的两倍,所以$P$在$BC$段速度为4个单位长度/秒,由
(1)可得动点$P$在$BC$段运动时间为$(t - 16.5)$秒,所以$BP = 4(t - 16.5)=4t - 66$.因为点$B$表示12,所以$P$表示的数为$12+(4t - 66)=4t - 54$.
查看更多完整答案,请扫码查看


