《2025年赢在假期期末加寒假七年级数学沪科版合肥工业大学出版社》

经典例题1　(内蒙古赤峰.中考)一个电子跳蚤在数轴上做跳跃运动.第一次从原点O起跳,落点为A₁,点A₁表示的数为1;第二次从点A₁起跳,落点为OA₁的中点A₂;第三次从A₂点起跳，落点为OA₂的中点A₃;如此跳跃下去……最后落点为OA₂₀₁₉的中点A₂₀₂₀，则点A₂₀₂₄表示的数为__________.
答案　$\frac{1}{2^{2023}}$
解析　由题意得，点A₁表示的数为$1 = \frac{1}{2^{0}}$，点A₂表示的数为$\frac{1}{2}OA_{1}=\frac{1}{2}=\frac{1}{2^{1}}$，点A₃表示的数为$\frac{1}{2}OA_{2}=\frac{1}{4}=\frac{1}{2^{2}}$，点A₄表示的数为$\frac{1}{2}OA_{3}=\frac{1}{8}=\frac{1}{2^{3}}$，…，归纳类推得，点Aₙ表示的数为$\frac{1}{2^{n - 1}}$（n为正整数），则点A₂₀₂₄表示的数为$\frac{1}{2^{2024 - 1}}=\frac{1}{2^{2023}}$，故答案为$\frac{1}{2^{2023}}$.

答案：

针对训练1　　已知点C在线段AB上,AC =2BC,点D,E在直线AB上,点D在点E 的左侧.若AB=18,DE=9,线段DE在线段AB上移动.
(1)如图1,当E为BC中点时,求AD的长;
(2)点F(异于点A,B,C)在线段AB上,AF =3AD,CE+EF=3,求AD的长.

答案： 针对训练1.解:
(1)因为AC=2BC,AB=18,所以AC+BC=2BC+BC=18,所以BC=6,AC=12.因为E为BC中点时，所以BE=$\frac{1}{2}$BC=3,所以BD=DE+BE=9+3=12,所以AD=AB−BD=18−12=6;
(2)当点E在点F的左侧，如图1，图2所示.
　CEFB图1　　　ECFB图2
因为CE+EF=CF=3,BC=6,所以BF=BC−CF=6 - 3=3,所以F是BC的中点,所以CF=BF=3,所以AF=AB−BF=18−3=15.因为AF=3AD,所以AD=$\frac{1}{3}$AF=$\frac{1}{3}$×15=5.因为CE+EF=3,所以图2这种情况求不出;
当点E在点F的右侧，如图3，图4所示.
ADFEC图3　　　ADCFEB图4
因为AC=12,CE+EF=CF=3,所以AF=AC−CF=12−3=9.因为AF=3AD,所以AD=$\frac{1}{3}$AF=$\frac{1}{3}$×9=3.因为CE+EF=3,所以图4这种情况求不出.
综上所述，AD的长为3或5.

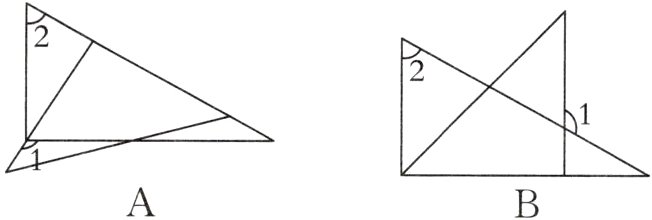
经典例题2　(黑龙江绥化.中考)将一副三角尺按如图方式进行摆放,∠1与∠2不一定互补的是 （ ）

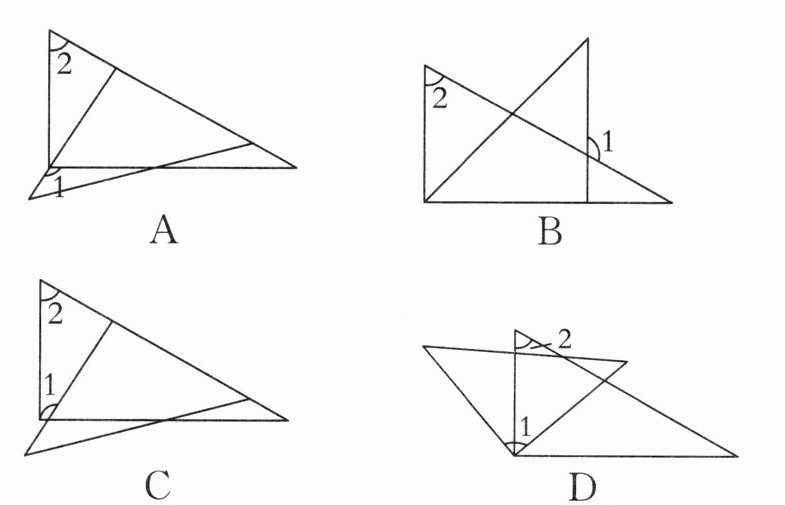
答案 D
解析　如图1,因为∠2 + ∠3 = 90°，∠3 + ∠4 = 90°，所以∠2 = ∠4. 因为∠1 + ∠4 = 180°，所以∠1 + ∠2 = 180°，所以∠1与∠2互补. 如图2，∠2 = ∠3，因为∠1 + ∠3 = 180°，所以∠1 + ∠2 = 180°，所以∠1与∠2互补. 如图3，因为∠2 = 60°，∠1 = 30° + 90° = 120°，所以∠1 + ∠2 = 180°，所以∠1与∠2互补. 如图4，因为∠1 = 90°，∠2 = 60°，所以∠1 + ∠2 = 90° + 60° = 150°，所以∠1与∠2不互补. 故选D.

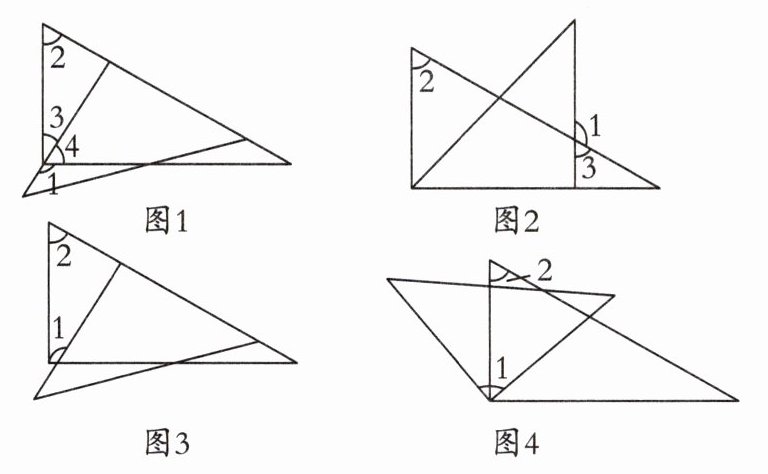
答案：