《2025年学霸六年级数学下册苏教版》

6. 如图，用一根彩带包扎一个长方体礼品盒，接头处的彩带长25厘米。这根彩带共有多长？

答案： 6. $(40 + 30)×2 + 20×4 + 25 = 245$（厘米）

7. 用一根铁丝正好可以围成一个棱长是6分米的正方体框架，如果用这根铁丝围成一个长是10分米、宽是5分米的长方体框架，高应是多少分米？

答案： 7. $6×12÷4 - 10 - 5 = 3$（分米）

8. 把12个圆柱形易拉罐放在一个长方体包装盒里，每个易拉罐的底面直径是6厘米，高是10厘米。你设计的长方体包装盒的长、宽、高各是多少厘米？请画出长方体包装盒草图并说明是怎样放置易拉罐的。

答案：
8. 长 24 厘米，宽 18 厘米，高 10 厘米

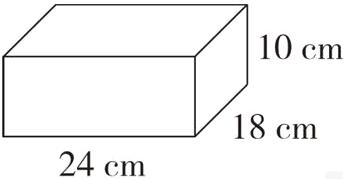
可以每排摆 4 个，摆 3 排（答案不唯一）
提示：12 个圆柱形易拉罐可以每排摆 4 个，摆 3 排，则长方体的长是 $6×4 = 24$（厘米），宽是 $6×3 = 18$（厘米），高（易拉罐的高）是 10 厘米，答案不唯一。

9. 一个长方体的长、宽、高分别为3厘米、2厘米、1厘米，一只蚂蚁从顶点A出发，沿棱爬行，如果要求不走重复路线，那么蚂蚁回到A点时，所走的最长路径是多少厘米？

答案： 9. $3×4 + 2×2 + 1×2 = 18$（厘米）
提示：要使蚂蚁所走的路径最长，可以从点 A 出发，在上面走 2 条长和 1 条宽，然后在后面走 1 条高，再在下面走 2 条长和 1 条宽，最后在前面走 1 条高回到出发点。这样一共走了 4 条长、2 条宽和 2 条高（路线不唯一）。

10. 朵朵把下面的木制模型的表面涂上颜色，正好可以将它分割成24个棱长是1厘米的小正方体。

(1)模型的表面积是( )平方厘米。
(2)按要求涂色的小正方体各有多少个？
4个面涂色：( )个；
3个面涂色：( )个；
2个面涂色：( )个；
1个面涂色：( )个；
0个面涂色：( )个。

答案：
10.
(1)54
(2)2 7 11 3 1
提示：如图，与标准的棱长是 3 厘米的正方体相比，拿掉几个小正方体的地方，几个面涂色的小正方体出现的位置有微妙的变化。

11. 如图，在每个正方体的六个面上分别写着1、2、3、4、5、6这六个数，并且任意两个相对的面上所写的两个数的和都等于7。现在把五个这样的正方体一个挨着一个地连接起来，在紧挨着的两个面上的两个数之和都等于8，那么图中打“?”的这个面上所写的数是( )。

答案：
11. 3
提示：如图，给正方体编号。从①号正方体开始推算：①号 1 的对面是 6；②号与①号紧挨的面是 2，2 的对面是 5；③号与②号紧挨的面是 3，3 的对面是 4。③号 1 的对面是 6，此时③号中数字 1、6、3、4 的位置已确定，所以③号与④号紧挨的面是 2 或 5。如果是 2，那么④号与③号紧挨的面是 6，6 的对面是 1；此时⑤号与④号紧挨的面应是 7，不符合题意。所以③号与④号紧挨的面是 5；④号与③号紧挨的面是 3，3 的对面是 4；⑤号与④号紧挨的面是 4，4 的对面是 3。

12. 如图是一张长方形硬纸，正好平均分成了15个小正方形。试把它们剪成3份，每份有5个小正方形相连，折起来都可以成为一个没有盖的正方体纸盒。(用彩笔在图中涂色表示)

答案：
12. 答案合理即可，如：

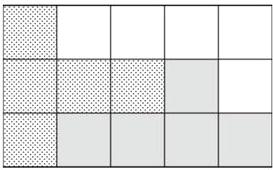
提示：根据题目要求和正方体展开图，进行涂色即可。