《2025年学霸六年级数学下册苏教版》

5. 如图，在仓库一角有一堆谷子，呈$\frac{1}{4}$圆锥形，量得底面弧长是1.57米，圆锥高为1米。每立方米谷子重约720千克，这堆谷子重约多少千克?（得数保留整数）

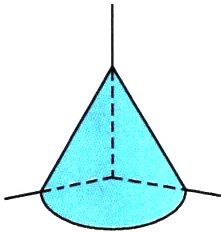
答案： $1.57×4÷3.14 = 2$（米） $\frac{1}{3}×3.14×(2÷2)^{2}×1×\frac{1}{4}×720≈188$（千克）

6. 如图，一块高是6厘米的圆锥形橡皮泥，从顶点沿着高将它切成两半后，表面积之和比原来增加了48平方厘米。这块圆锥形橡皮泥的体积是多少立方厘米?

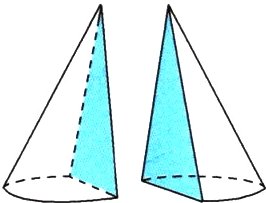
答案： $48÷2 = 24$（平方厘米） $24×2÷6 = 8$（厘米）
$3.14×(8÷2)^{2}×6×\frac{1}{3}=100.48$（立方厘米）

7. 一个圆柱形容器的底面直径是10厘米，高是12厘米，容器内水深11厘米。把一个底面半径是4厘米，高是9厘米的圆锥形铁块放入容器中，会溢出多少毫升的水?

答案： $3.14×4^{2}×9×\frac{1}{3}-3.14×(10÷2)^{2}×(12 - 11)=72.22$（立方厘米） 72.22立方厘米 = 72.22毫升

8. 如图，将直角梯形ABCD以高AB所在直线为轴旋转一周，形成一个圆台，求它的体积。

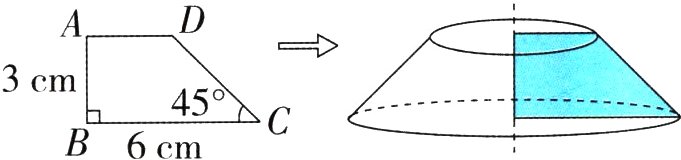
答案： $\frac{1}{3}×3.14×6^{2}×6 = 226.08$（立方厘米）
$6 - 3 = 3$（厘米）
$\frac{1}{3}×3.14×3^{2}×3 = 28.26$（立方厘米）
$226.08 - 28.26 = 197.82$（立方厘米）

9. 如图，圆锥形容器的底面半径是圆柱形容器底面半径的一半，圆锥形容器的高是圆柱形容器高的$\frac{1}{3}$。现用圆锥形容器盛满水，倒入空的圆柱形容器中，倒了6次后，圆柱形容器中的水深是多少厘米?

答案： $1^{2}:2^{2}=1:4$ $(1×1×\frac{1}{3}):(4×3)=1:36$
$(1×6)÷36=\frac{1}{6}$ $24×\frac{1}{6}=4$（厘米）
提示：先根据圆锥形容器与圆柱形容器底面半径的比求出底面积的比是 $1^{2}:2^{2}=1:4$，再根据底面积的比和高的比求出体积比是 $(1×1×\frac{1}{3}):(4×3)=1:36$。再求倒6次后圆柱形容器中水的体积占容积的 $(1×6)÷36=\frac{1}{6}$，最后求出水深为 $24×\frac{1}{6}=4$（厘米）。

10. 如图，一个直角三角形三条边的长分别为3厘米、4厘米和5厘米，以斜边所在直线为轴旋转一周形成了一个立体图形，则这个立体图形的体积是多少立方厘米?

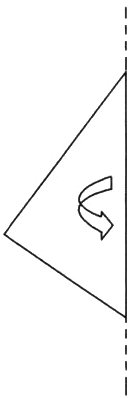
答案：
$3×4÷2×2÷5 = 2.4$（厘米）
$3.14×2.4^{2}×5×\frac{1}{3}=30.144$（立方厘米）
提示：如图，直角三角形以斜边所在直线为轴旋转一周所形成的立体图形是由两个圆锥组成的，它们的底面相同。先求出直角三角形斜边上的高（也就是圆锥的底面半径）为 $3×4÷2×2÷5 = 2.4$（厘米）。假设上面圆锥的高是 $h_{1}$，下面圆锥的高是 $h_{2}$，则 $h_{1}+h_{2}=5$厘米。形成的立体图形的体积为 $3.14×2.4^{2}×h_{1}×\frac{1}{3}+3.14×2.4^{2}×h_{2}×\frac{1}{3}=3.14×2.4^{2}×(h_{1}+h_{2})×\frac{1}{3}=3.14×2.4^{2}×5×\frac{1}{3}=30.144$（立方厘米）。

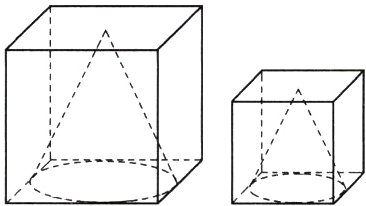
11.（假设思想）两个正方体木块的体积之差为4104立方厘米，如果以正方体的一面为底面加工成最大的圆锥(如图所示)，那么加工成的两个圆锥的体积之差是多少立方厘米?

答案：
设大正方体的棱长为 $2x(x＞0)$厘米，则其一面的面积为 $4x^{2}$平方厘米，其内部最大的圆锥的底面直径为 $2x$厘米，底面积为 $3.14x^{2}$平方厘米，则圆锥的底面积是正方体底面积的 $\frac{3.14x^{2}}{4x^{2}} = 78.5\%$
$4104×78.5\%×\frac{1}{3}=1073.88$（立方厘米）
提示：假设大正方体的体积为 $a$立方厘米，小正方体的体积为 $b$立方厘米，则 $a - b = 4104$。先将两个正方体加工成最大的圆柱(如图)，再加工成最大的圆锥。从图中可以看出，圆柱的底面是正方体底面中最大的圆，则圆柱(圆锥)的底面积是正方体底面积的78.5%；由于圆柱的高与正方体的高相等，所以圆柱的体积是正方体体积的78.5%。两个圆柱的体积之差为 $a×78.5\% - b×78.5\%$，而加工成的最大圆锥是圆柱体积的 $\frac{1}{3}$，所以两个圆锥的体积之差为 $a×78.5\%×\frac{1}{3}-b×78.5\%×\frac{1}{3}=(a - b)×78.5\%×\frac{1}{3}=4104×78.5\%×\frac{1}{3}=1073.88$（立方厘米）。