《2025年学霸六年级数学下册苏教版》

（2）如果圆柱的高是5分米，长方体的表面积比圆柱增加了20平方分米。这个圆柱的体积是(　　　)立方分米。

答案： 7.
(2)62.8

（3）如果圆柱的底面半径是4厘米，侧面积是251.2平方厘米，乐乐把长方体侧放后，如图，他快速地求出了圆柱的体积是(　　　)立方厘米。

答案： 7.
(3)502.4

8. 如图，有一瓶水，瓶底的半径是5厘米，将瓶正放，水面高16厘米；将瓶倒放，水面离瓶底还有4厘米，求瓶子的容积。

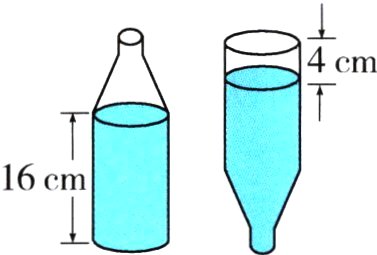
答案： 8. $3.14\times5^{2}\times(16 + 4) = 1570$(立方厘米)
1570立方厘米 = 1570毫升 = 1.57升

9. 在一个圆柱形水桶里，放进一段截面半径是5厘米的圆钢(圆柱形)，如果圆钢全部浸在水中(水未溢出)，那么水桶里的水面上升10厘米；如果把水中的圆钢竖着提起，使它露出水面6厘米，那么水桶里的水面就下降2厘米。求这段圆钢的体积。

答案： 9. $3.14\times5^{2}\times(10\div2\times6) = 2355$(立方厘米)

10. 如图，用一张边长为82.8厘米的正方形卡纸做一个尽可能长的圆柱形包装盒后，剩余边角料的面积是多少？包装盒的体积是多少(用含$\pi$的式子表示)？
　　　　　　　　　　

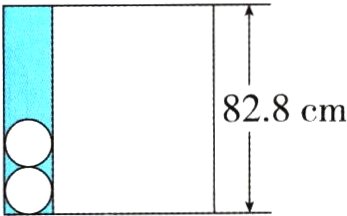
答案： 10. $82.8\div(1 + 3.14) = 20$(厘米)
$82.8\times20 - 2\times3.14\times(20\div2)^{2} = 1028$(平方厘米)
$\pi\times(20\div2)^{2}\times82.8 = 8280\pi$(立方厘米)

11.（转化思想）如图，一个圆柱形物体的底面直径是8分米，被斜截后，最低处高是10分米，最高处高是15分米。被截后的物体体积是多少立方分米?

答案： 11. $3.14\times(8\div2)^{2}\times(10 + 15)\div2 = 628$(立方分米)
提示：假设被斜截去的部分与剩下的部分完全相同，即在现在这个立体图形上补充一个与之完全相同的图形，拼成一个底面直径是8分米、高是$(10 + 15)$分米的圆柱，先求出这个圆柱的体积，再求出它的一半，就是被截后的物体的体积。

12. 一根圆柱形木料，如果按图①所示切成完全相同的4块，表面积会增加600平方厘米；如果按图②所示切成完全相同的3块，表面积会增加314平方厘米。求这根木料的体积。
　　　　　　　　

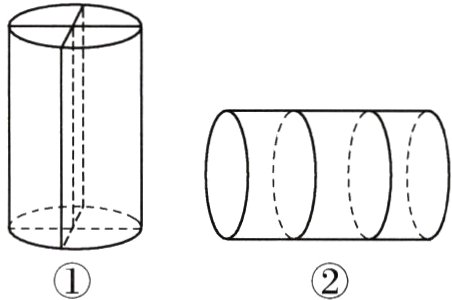
答案： 12. 圆柱的底面积：$314\div4 = 78.5$(平方厘米)
底面半径的平方：$78.5\div3.14 = 25$(平方厘米)
由于$5\times5 = 25$，所以底面半径为5厘米
圆柱的高：$600\div4\div(5\times2) = 15$(厘米)
圆柱的体积：$78.5\times15 = 1177.5$(立方厘米)
提示：按题图①所示的切法，表面积增加的部分可以看成是4个长方形，每个长方形的面积等于底面直径与高的乘积。每个长方形的面积为$600\div4 = 150$(平方厘米)。按题图②所示的切法，表面积增加的部分是4个底面面积。圆柱的底面面积为$314\div4 = 78.5$(平方厘米)，则$r^{2}=78.5\div3.14 = 25$(平方厘米)，进而推算出$r = 5$厘米。圆柱的高为$150\div(5\times2) = 15$(厘米)，则圆柱的体积为$78.5\times15 = 1177.5$(立方厘米)。

13. 小明用橡皮泥做了一个圆柱，他发现如果圆柱的底面直径增加2厘米，高不变，它的侧面积就增加62.8平方厘米。如果它的高增加3厘米，底面直径不变，它的侧面积就增加18.84平方厘米。这个圆柱原来的体积是多少立方厘米?

答案： 13. 圆柱的高：$62.8\div(3.14\times2) = 10$(厘米)
圆柱的底面半径：$18.84\div3\div3.14\div2 = 1$(厘米)
圆柱的体积：$3.14\times1^{2}\times10 = 31.4$(立方厘米)
提示：根据条件可分别求出圆柱的高和底面半径，然后再求原来圆柱的体积。