《2025年学霸六年级数学下册苏教版》

5.（1）如图，把长方形的纸这样折起来以后，已知∠1=30°，∠2=20°，∠3=(　　　)°。

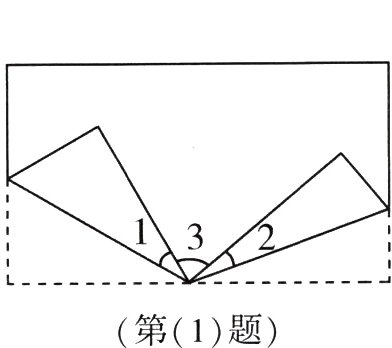
答案： 80

（2）如图，O为圆心，点A、点B、点C将圆等分成三份，∠1=(　　　)°，∠2=(　　　)°。

答案： 120 30

（3）如图，将等腰三角形纸片剪去顶角后得到一个四边形，∠1+∠2=(　　　)°。

答案： 220

（4）用等腰直角三角形画出∠AOB = 45°，并将三角尺沿OB方向平移到如图所示的虚线处后，再绕点M向逆时针方向旋转30°，则三角尺的斜边与射线OA的夹角α的度数是(　　　)。

答案： 30°

（5）如图，已知图中最大的角是直角，∠2 = 15°，则图中所有锐角的和是(　　　)°。

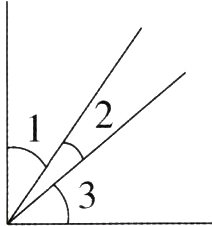
答案： 195

6.（1）如图，小梅家、小兰家和小芳家附近有一个汽车站，现在要经过汽车站修一条公路，使她们三家到这条公路的距离都相等，应该怎样修？画一画。

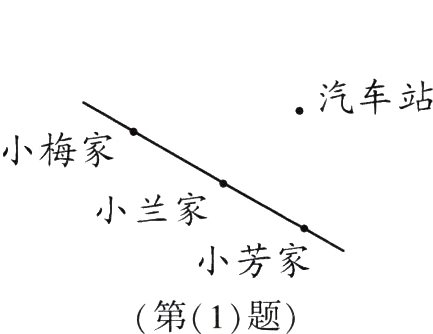
答案：
使她们三家到这条公路的距离都相等，应过汽车站作已知直线的平行线，如图所示。

（2）小鸭擅长游泳，在岸上行走却很吃力。它想从A点到河对岸的B点去。你能帮它设计一条最省力的路线吗？画一画。

答案：
由于小鸭擅长游泳，在岸上行走却很吃力，所以应从A、B两点向河岸分别作两条直线的垂直线段，然后把两个垂足连起来，如图所示。这样就能保证小鸭在岸上行走的路线最短，最省力。

7. 正方形网格中，小方格的顶点叫作格点。图中每个小方格都是边长为1的正方形，A、B两点在正方形网格的格点上，点C也在格点上，且三角形ABC为等腰三角形，则符合条件的格点C共有(　　　)个。(请把这些点标出来)

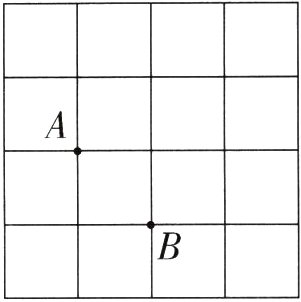
答案：
9

提示：符合条件的格点C共有9个，这样的点分两类：以AB为等腰三角形的底，这样的点有5个；以AB为等腰三角形的腰，这样的点有4个。

8. 两条直线相交 三条直线相交 四条直线相交
最多一个交点 最多三个交点 最多六个交点

（1）猜想并验证：五条直线相交最多(　　　)个交点，比四条直线相交多(　　　)个交点。
（2）10条直线相交最多有(　　　)个交点。

答案：
(1)10 4
(2)45
提示：每增加一条直线，最多与先前的每条直线相交一次，即n条直线相交，最多有[1 + 2 + 3 + ⋯ + (n - 1)]个交点。

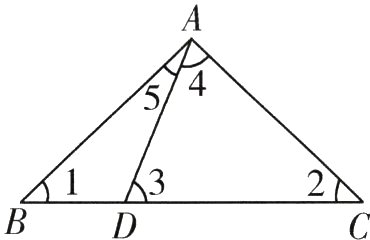
9. 等量代换 如图，在三角形ABC中，点D在BC上，且∠1 = ∠2，∠3 = ∠4，∠5 = 24°，求∠1的度数。

答案：
(180° - 24°×2)÷3 = 44°
提示：如图，设与∠3相邻的角为∠6。从图中可以看出，∠1 + ∠5 + ∠6 = 180°，∠3 + ∠6 = 180°，则∠3 = ∠1 + ∠5。由于∠3 = ∠4，则∠4 = ∠1 + ∠5。又因为∠1 = ∠2，则三角形ABC的内角和∠1 + ∠2 + ∠4 + ∠5 = ∠1 + ∠1 + ∠1 + ∠5 + ∠5 = 180°，所以用180°减去2个∠5的度数和，然后再除以3，就可以求出∠1的度数。

10. 如图，在一个圆上有5个点，经过每三个点可以画一个三角形，一共可以画出多少个三角形？

答案： 6 + 3 + 1 = 10(个)
提示：假设圆上的五个点分别是A、B、C、D、E，则组成的三角形有三角形ABC、三角形ABD、三角形ABE、三角形ACD、三角形ACE、三角形ADE、三角形BCD、三角形BCE、三角形BDE、三角形CDE。