《2026年薪火金卷高考仿真模拟卷物理》

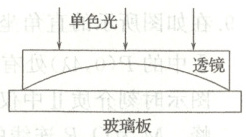
4. 用牛顿环可测量平凹透镜球面的曲率半径。如图所示,平凹透镜与一
块平板玻璃接触,用单色光垂直于透镜的平面向下照射,会观察到明暗
相间的同心圆环,根据圆环半径可计算出球面的曲率半径$R$,则

A.形成同心圆环属于光的色散现象
B.同心圆环内疏外密
C.曲率半径$R$越大,圆环越紧密
D.圆环疏密程度与透镜的折射率有关

答案： 4.B　[同心圆环由光的叠加原理形成，属于光的薄膜干涉现象，故A错误;明暗相间的同心圆环是由透镜和玻璃板之间的空气膜上下两表面的反射光发生干涉后形成的，同一亮圆环(或暗圆环)处空气膜的厚度相等，相邻的两个亮圆环处，空气膜的厚度差等于半个波长，离圆心越远的位置，空气膜的厚度减小得越快，则圆环越密，所以同心圆环内疏外密，故B正确;透镜的曲率半径$R$变大，空气膜的厚度变化越慢，其形成的圆环比曲率半径小的透镜形成的圆环稀疏，故C错误;圆环由薄膜干涉原理形成，其疏密程度与光的波长及空气膜的厚度变化情况有关，与透镜的折射率无关，故D错误。故选B。]

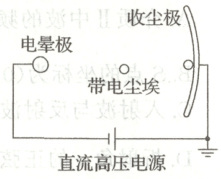
5. 静电除尘器装置的示意图如图所示。尘埃在电场中通过某种机制带电,
在电场力的作用下向收尘极迁移并沉积,以达到除尘目的。则

A.带电尘埃带正电荷
B.电场方向由电晕极指向收尘极
C.带电尘埃在运动过程中加速度变小
D.若电源正、负极对调,尘埃将沉积在电晕极

答案： 5.C　[由题图可知，收尘极为正极，因异极相吸，所以到达收尘极的尘埃带负电荷，故A错误;收尘极与电源正极相连，电场方向由收尘极指向电晕极，故B错误;除尘器内电场线为电晕极密、收尘极疏，尘埃向收尘极迁移过程中电场强度越来越小，其受到的电场力越来越小,根据牛顿第二定律$F = ma$可知,带电尘埃在运动过程中的加速度变小，故C正确;若电源正、负极对调，带电尘埃由于电晕极放电将带上正电荷，仍将向收尘极运动，故D错误。]

6. 如图所示,一个正四棱锥形框架放置在地面上,各侧棱边长和底边的对角线长均为$L$,在各侧棱都有轻质光滑圆环,对侧圆环被同一根弹性绳连接,在弹性绳的交叉点穿过一个轻质小圆环,其半径忽略不计。在环上用轻质硬绳挂一个质量为$m$的重物,初始时由于重物被手托举,弹性绳均处于各侧棱的中点位置,若整个过程中都处于弹性限度内,弹性绳的劲度系数均为$k$,弹性势能$E_p=\frac{1}{2}k\Delta x^2$,则自由释放重物以后


A.重物下落过程中,该重物的机械能守恒
B.重物下落过程中,各侧棱的轻质小环不会运动
C.重物下落过程中,重物的最大速度为$\sqrt{\frac{mg^2}{2k}+\frac{2-\sqrt{3}}{2}gL}$
D.重物下落到最低点时,弹性绳对重物做的功为$\frac{m^2g^2}{2k}+\frac{2-\sqrt{3}}{4}mgL$

答案： 6.C　[重物下落过程中,弹性绳对重物要做功，所以重物的机械能不守恒，故A错误;重物下落过程中，侧棱上的轻质小环会有一定的下降，故B错误;重物下落过程中，由于轻质小环和侧棱之间是光滑的，释放重物后，由于小环轻质，重物下落至任何位置，绳与侧棱均垂直，设每根弹性绳的长度是$x$，则经分析，交叉点到棱尖$S$的距离也为$x$；环是轻质的，故可知初始弹性绳处于原长状态，当重物速度最大时，有$4k(x - \frac{L}{2})\cos 60^{\circ} = mg$，解得$x = \frac{mg}{2k} + \frac{L}{2}$，由机械能守恒定律，得$mg(x - \frac{\sqrt{3}}{4}L) = \frac{1}{2}mv^{2}_{m} + 2×\frac{1}{2}k(x - \frac{1}{2}L)^{2}$，解得重物的最大速度为$v_{m} = \sqrt{\frac{mg^{2}}{2k} + \frac{2 - \sqrt{3}}{2}gL}$，此过程重力对重物做的功为$W_{G} = mg(x - \frac{\sqrt{3}}{4}L) = \frac{m^{2}g^{2}}{2k} + \frac{2 - \sqrt{3}}{4}mgL$，到最低点的过程重力继续对重物做功，有$W'_{G} ＞ W_{G}$，在最低点速度为零，根据动能定理可知重物下落到最低点时，弹性绳对重物做的功$W_{弹} = -W_{G}$，故C正确,D错误。]

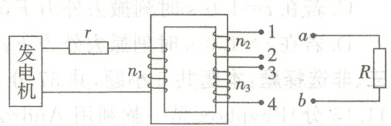
7. 如图所示,发电机输出电压峰值一定的正弦式交流电,接入理想变压器原线圈,导线电阻$r=2\ \Omega$,原线圈匝数$n_1=50$,副线圈有两个绕组,匝数分别为$n_2=50$、$n_3=150$,负载定值电阻$R=8\ \Omega$。下列不同连接方式中,电阻$R$功率最大的是


A.$a$端接1,$b$端接2
B.$a$端接3,$b$端接4
C.2、3连接,$a$端接1,$b$端接4
D.1、3连接,$a$端接2,$b$端接4

答案：
7.D　[如图所示，将变压器及右侧部分等效为一个电阻$R'$，当$a、b$端与副线圈绕组按不同方式连接时，副线圈等效匝数设为$n'_{2}$，设原线圈两端电压、流过的电流分别为$U_{1}、I_{1}$，电阻$R$两端的电压、流过的电流分别为$U_{2}、I_{2}$，则有$R' = \frac{U_{1}}{I_{1}} = \frac{\frac{n_{1}}{n'_{2}}U_{2}}{\frac{n'_{2}}{n_{1}}I_{2}} = \frac{n^{2}_{1}}{n'^{2}_{2}}\frac{U_{2}}{I_{2}} = \frac{n^{2}_{1}}{n'^{2}_{2}}R$，设发电机输出电压有效值为$E$，等效电阻$R'$的功率为$I^{2}_{1}R' = (\frac{E}{r + R'})^{2}R' = \frac{E^{2}}{\frac{r^{2}}{R'} + R' + 2r}$，当$\frac{r^{2}}{R'} = R'$时，等效电阻$R'$的功率$P'$有最大值，此时$R' = r$。当$a$端接1，$b$端接2时，副线圈等效匝数为$n_{2} = 50$，$R' = \frac{n^{2}_{1}}{n^{2}_{2}}R = 8\ \Omega$；当$a$端接3，$b$端接4时，副线圈等效匝数为$n_{3} = 150$，$R' = \frac{n^{2}_{1}}{n^{2}_{3}}R = \frac{8}{9}\ \Omega$；当2、3连接，$a$端接1，$b$端接4时，副线圈等效匝数为$n_{3} + n_{2} = 200$，$R' = \frac{n^{2}_{1}}{(n_{3} + n_{2})^{2}}R = \frac{1}{2}\ \Omega$；当1、3连接，$a$端接2，$b$端接4时，副线圈等效匝数为$n_{3} - n_{2} = 100$，$R' = \frac{n^{2}_{1}}{(n_{3} - n_{2})^{2}}R = 2\ \Omega$，此时$R' = r$，等效电阻$R'$的功率$P'$有最大值，即电阻$R$的功率最大。故选D。]
　　　　　　　　　　　　

8. 如图甲所示,活塞将一定质量的理想气体封闭在汽缸内。设法让汽缸中的气体经历$A\to B\to C\to D$的变化,气体的压强与摄氏温度的关系如图乙中实线所示。图乙中$O$为坐标原点,$A$在$p$轴上,$AB// DC$,$BC// AO$,$AD// t$轴,$BA$的延长线经过$(-273.15,0)$,$CD$的延长线经过$O$。关于气体各个阶段的情况,下列说法正确的是


A.$A\to B$和$C\to D$气体都做等容变化
B.从$C$到$D$,气体的分子数密度逐渐减小
C.从$B$到$C$,气体从外界吸收热量
D.从$A$到$D$全过程,外界对气体做正功

答案：
8.BC　[根据理想气体状态方程可得$p = \frac{C}{V}· T$，$A \to B$延长线过绝对零度，为等容线，气体做等容变化，对比发现$C$与绝对零度的连线和$D$点与绝对零度的连线，斜率减小，故体积$V$变大，$C \to D$气体体积变大，A错误;结合$A$可知，从$C$到$D$，气体体积变大，分子数密度逐渐减小，B正确;从$B$到$C$，气体等温降压，可知内能不变，体积增大对外做功，故气体必须从外界吸收热量，C正确;从$A$到$B$体积不变，气体没有做功，从$B$到$C$气体对外做功，从$C$到$D$气体对外做功，从$D$到$A$等压降温，体积减小，外界对气体做功，如图所示为改画的$p - V$图线，图线和横轴所围的面积表示气体做的功，可知气体对外做功大于外界对气体做的功，故整个过程气体对外做正功，D错误。]