《2026年薪火金卷高考仿真模拟卷物理》

4. 两颗中子星绕二者连线上的某点做圆周运动组成双星系统,并以引力波的形式向外辐射能量。经过一段时间,两颗中子星的间距减小为原来的$p$倍,运行周期变为原来的$q$倍。若两星可视为质量均匀分布的球体,则利用牛顿力学知识可得

A.$p^2q^3=1$
B.$\frac{p^2}{q^3}=1$
C.$p^3q^2=1$
D.$\frac{p^3}{q^2}=1$

答案： 4.D [设两颗中子星的质量分别为$m_1$、$m_2$，轨道半径分别为$r_1$、$r_2$，相距$L$，运行周期为$T$，根据万有引力提供向心力可知$\frac{Gm_1m_2}{L^2}=m_1\frac{4\pi^2}{T^2}r_1$，$\frac{Gm_1m_2}{L^2}=m_2\frac{4\pi^2}{T^2}r_2$，又$L = r_1 + r_2$，联立可得$\frac{G(m_1 + m_2)}{4\pi^2}=\frac{L^3}{T^2}$，依题意，两颗中子星的间距减小为原来的$p$倍，运行周期变为原来的$q$倍，则有$\frac{G(m_1 + m_2)}{4\pi^2}=\frac{(pL)^3}{(qT)^2}$，联立解得$\frac{p^3}{q^2}=1$。故选D。]

5. 人体的细胞膜由磷脂双分子层组成,双分子层之间存在电压(医学上称为膜电位),使得只有带特定电荷的粒子才能通过细胞膜进入细胞内,如图所示。初速度为零的正一价钠离子仅在电场力的作用下,从细胞膜外$A$点运动到细胞膜内$B$点,则下列说法正确的是()

A.$A$点电势低于$B$点电势
B.从$A$点运动到$B$点,钠离子的电势能增大
C.若膜电位不变,当$d$增大时,钠离子的加速度变小
D.若膜电位不变,当$d$增大时,钠离子进入细胞内的速度变大

答案： 5.C [钠离子受力方向从$A$指向$B$，所以电场线方向也是从$A$指向$B$，沿电场线方向电势逐渐降低，所以$A$点的电势高于$B$点的电势，故A错误；钠离子从$A$点到$B$点，电场力做正功，钠离子的电势能减小，故B错误；若膜电位不变，即$A$、$B$间的电压不变，当$d$增大时，由$E = \frac{U}{d}$可知，电场强度变小，钠离子受到的电场力变小，根据牛顿第二定律知，钠离子的加速度变小，故C正确；若膜电位不变，根据动能定理有$qU = \frac{1}{2}mv^2$，可知钠离子进入细胞内的速度不变，故D错误。]

6. 水平轨道固定在地面上,右侧固定一磁铁,如图甲所示。右端粘有磁铁的小车以初速度$v_0$沿轨道向右运动,两磁铁间有相互排斥的作用力。某科研兴趣小组利用该实验装置研究小车在变力作用下的运动情况。无线传感器记录作用过程中小车的$v-t$图像(如图乙所示)以及小车所受斥力大小$F$随时间$t$的变化图像(如图丙所示)。已知小车所受摩擦阻力及空气阻力远小于磁铁间的相互作用力。那么( )


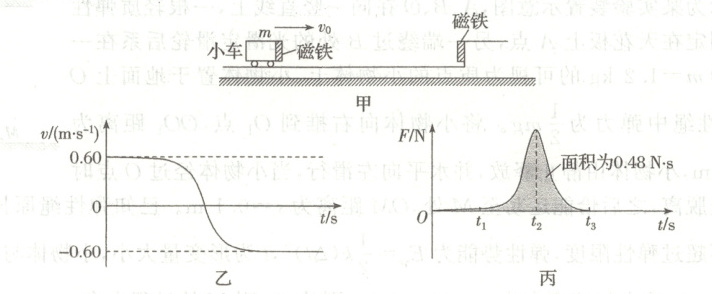
A.小车速度为零时,其所受合外力也恰好为零
B.小车在$t_1$到$t_2$向右做匀减速直线运动,$t_2$到$t_3$向左做匀加速直线运动
C.小车与固定在轨道上的磁铁相互作用过程中,小车的机械能守恒
D.小车质量$m$约为$400 g$

答案： 6.D [由题图乙可知，小车速度为零时，加速度最大，此刻所受合外力最大，故A错误；由题图丙可知，小车在$t_1\sim t_2$时间内受到的磁铁的力逐渐增大，向右做加速度逐渐增大的减速直线运动，在$t_2\sim t_3$时间内受到的磁铁的力逐渐减小，向左做加速度逐渐减小的加速直线运动，故B错误；根据题图乙可知，小车与固定在轨道上的磁铁相互作用过程中，动能先减小后增大，故其机械能先减小后增大，故C错误；小车在$t_1\sim t_3$时间内，根据动量定理公式可得$-Ft = -mv_0 - mv_0$，又因为$F - t$图像的面积表示冲量，可得$0.48\ N·s=2m×0.60\ m/s$，解得$m = 0.4\ kg=400\ g$，故D正确。]

7. 如图,两足够长、电阻不计的光滑金属轨道$EAB$、$FCD$平行放置,两导轨间距为$L$,$AB$、$CD$与水平面的夹角$\theta=60°$,左侧部分水平。质量分别为$2m$、$m$,阻值分别为$2R$、$R$的两金属棒$p$、$q$分别置于倾斜轨道与水平轨道上,整个空间存在磁场,右侧为磁感应强度大小为$B=\sqrt{\frac{mgR}{L^2v}}$($v$为一已知定值)、方向垂直于倾斜导轨向上的匀强磁场$B_1$,左侧为磁感应强度大小为$2B$、方向与$B_1$的方向相反的匀强磁场$B_2$。现静止释放$p$棒,运动过程中两棒始终与金属轨道垂直且接触良好。重力加速度为$g$,经过足够长的时间后,下列说法正确的是()

A.金属棒$q$最终将停下
B.金属棒$p$最终将匀速下滑
C.金属棒$p$的加速度为$a_p=\frac{\sqrt{3}}{6}g$
D.金属棒$q$的加速度为$a_q=\frac{\sqrt{3}}{3}g$

答案： 7.D [静止释放$p$棒，根据右手定则可知，$p$棒中感应电流的方向向外，$q$棒中感应电流的方向向里，根据左手定则可知，$p$棒所受安培力的方向沿斜轨道向上，$q$棒所受安培力的方向垂直于$B_2$斜向左上方，两棒均开始做加速运动，两棒切割磁感线产生的感应电动势方向相反，回路总感应电动势为$E = B_1Lv_p - B_2Lv_q\cos\theta = BL(v_p - v_q)$，回路中的感应电流$I = \frac{E}{2R + R}=\frac{BL(v_p - v_q)}{3R}$。开始时，两棒速度差较小，感应电流较小，安培力较小，则$p$棒加速度较大，$q$棒加速度较小，即$p$棒比$q$棒加速得快一些，两者速度差增大，感应电流增大，$p$棒加速度减小，而$q$棒加速度增大，当两者加速度大小相等时，两者速度差一定，此时感应电流一定，安培力也一定，两者开始做匀加速直线运动，令加速度大小为$a$，根据牛顿第二定律有$2mg\sin\theta - B_1IL = 2ma$，$B_2IL\cos\theta = ma$，解得$a = \frac{\sqrt{3}}{3}g$，即最终两棒的加速度均为$\frac{\sqrt{3}}{3}g$。故选D。]