《2026年薪火金卷高考仿真模拟卷物理》

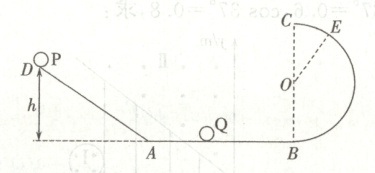
15. (19分)如图所示，表面光滑的固定斜面与水平面的夹角$\theta = 37°$，斜面底端与水平光滑轨道$AB$平滑连接，水平轨道右端$B$点连接竖直的光滑半圆轨道，半圆轨道的圆心为$O$，最高点为$C$，半径$R = 0.5 m$。有一质量$m_P = 1 kg$的小球P以$v_0 = \sqrt{70} m/s$的初速度从斜面上的$D$点沿斜面向下运动，到达水平轨道$AB$后与静止在水平轨道上的小球$Q$发生碰撞，碰撞后，小球$Q$恰好沿水平轨道运动到半圆轨道的$E$点，$\angle COE = 37°$。已知$D$点距地面的高度$h = 0.9 m$，小球P、$Q$均可看作质点，重力加速度$g$取$10 m/s^2$，$\sin 37° = 0.6$，$\cos 37° = 0.8$，计算结果可以保留根号。求：

(1)小球P与小球Q碰前的速度大小；
(2)小球Q运动过程中，上升的最大高度；
(3)碰撞后小球Q的速度大小。

答案： 15.解析
(1)设小球$P$运动到水平轨道的速度为$v_{1}$，故小球$P$在沿斜面向下运动的过程中，由动能定理可得$m_{P}gh=\frac{1}{2}m_{P}v_{1}^{2}-\frac{1}{2}m_{P}v_{0}^{2}$，解得$v_{1}=2\sqrt{22}m/s$。
(2)当小球$Q$运动到$E$点时，设小球$Q$的质量为$m_{Q}$，速度为$v_{E}$，小球只受重力，受力分析如图所示:根据重力的分力提供向心力得$m_{Q}g\cos37^{\circ}=m_{Q}\frac{v_{E}^{2}}{R}$，解得$v_{E}=2m/s$，小球$Q$经过$E$点之后做斜抛运动，设竖直方向的速度为$v_{y}$，根据速度的合成与分解可得$v_{y}=v_{E}\sin37^{\circ}$，解得$v_{y}=1.2m/s$，由运动学公式可得，小球$Q$竖直方向减速到零，距$E$点的高度$h_{1}=\frac{v_{y}^{2}}{2g}$，解得$h_{1}=0.072m$，所以小球$Q$上升的最大高度$h_{Q}=R(1+\cos37^{\circ})+h_{1}$，解得$h_{Q}=0.972m$。
(3)设两球发生弹性碰撞后小球$Q$的速度大小为$v_{Q}$，碰撞后小球$Q$运动到$E$点的过程，根据动能定理可得$m_{Q}gR(1+\cos37^{\circ})=\frac{1}{2}m_{Q}v_{Q}^{2}-\frac{1}{2}m_{Q}v_{E}^{2}$，解得$v_{Q}=\sqrt{22}m/s$。
答案
(1)$2\sqrt{22}m/s$
(2)$0.972m$
(3)$\sqrt{22}m/s$