《2026年薪火金卷高考仿真模拟卷物理》

13. (9分)差压阀可控制气体进行单向流动,广泛应用于减震系统。如图所示,$A$、$B$两个导热良好的汽缸通过差压阀连接,$A$内轻质活塞的上方与大气连通,$B$的体积不变。当$A$内气体压强减去$B$内气体压强大于$\Delta p$时差压阀打开,$A$内气体缓慢进入$B$中;当该差值小于或等于$\Delta p$时差压阀关闭。当环境温度$T_1=300 K$时,$A$内气体体积$V_{A1}=4.0×10^{-2} m^3$;$B$内气体压强$p_{B1}$等于大气压强$p_0$。已知活塞的横截面积$S=0.10 m^2$,$\Delta p=0.11p_0$,$p_0=1.0×10^5 Pa$。重力加速度大小取$g=10 m/s^2$,$A$、$B$内的气体可视为理想气体,忽略活塞与汽缸间的摩擦,差压阀与连接管道内的气体体积不计。当环境温度降低到$T_2=270 K$时,

(1)求$B$内气体压强$p_{B2}$;
(2)求$A$内气体体积$V_{A2}$;
(3)在活塞上缓慢倒入铁砂,若$B$内气体压强回到$p_0$并保持不变,求已倒入铁砂的质量$m$。

答案： 13.解析　
(1)对$B$内的气体进行分析，假设$A$汽缸中的气体并未进入到$B$汽缸中，则$B$汽缸中的气体发生等容变化，根据查理定律可得$\frac{p_0}{T_1}=\frac{p_{B2}}{T_2}$，
解得$p_{B2} = 0.9p_0$，
此时，$A$汽缸的气体与$B$汽缸的气体压强差为$\Delta p_1 = p_0 - p_{B2} = p_0 - 0.9p_0 = 0.1p_0 ＜ \Delta p = 0.11p_0$，
假设成立。
(2)结合上述分析可知，$A$汽缸中的气体发生等压变化，根据盖一吕萨克定律可得$\frac{V_{A1}}{T_1}=\frac{V_{A2}}{T_2}$，
解得$V_{A2} = 3.6×10^{-2}\ m^3$。
(3)若$B$内气体压强回到$p_0$并保持不变，则说明此时$A$汽缸的压强为$p_{A2} = p_0 + \Delta p = 1.11p_0$，
此时对活塞进行受力分析可得$mg + p_0S = p_{A2}S$，
代入数据解得$m = 110\ kg$。
答案
(1)$0.9p_0$
(2)$3.6×10^{-2}\ m^3$
(3)$110\ kg$

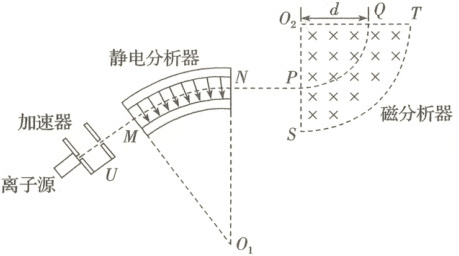
14. (14分)某“双聚焦分析器”质谱仪工作原理如图所示,加速器中加速电压为$U$,静电分析器中有辐向电场,即与圆心$O_1$等距各点的电场强度大小相同,方向指向圆心$O_1$。磁分析器中以$O_2$为圆心、圆心角为$90°$的扇形区域内,分布着方向垂直于纸面向里的匀强磁场,其左边界$O_2S$与静电分析器的右边界平行。离子源逸出初速度为$0$、质量为$m$、电荷量为$q$的正离子,经加速电场加速后,从$M$点垂直于$O_1M$进入静电分析器,沿半径为$R$的圆弧轨道做匀速圆周运动,后从$N$点射出,然后离子由垂直于$O_2S$射入磁分析器中,最后离子垂直于$O_2T$从$Q$点射出。已知$O_2Q=d$,$O_2T=\sqrt{3}d$,不计离子重力及离子间的相互作用。

(1)求离子从加速器射出时速度$v$的大小;
(2)求静电分析器中离子运动轨迹处电场强度$E$的大小;
(3)若离子源逸出初速度为$0$、比荷不同的正离子,求能从磁场区域上边界$O_2T$出射的离子比荷$k$的范围。

答案：
14.解析　
(1)离子经电场直线加速，由动能定理有$qU = \frac{1}{2}mv^2$，
解得$v = \sqrt{\frac{2qU}{m}}$。
(2)离子在静电分析器中做匀速圆周运动，根据牛顿第二定律，有$qE = m\frac{v^2}{R}$，
解得$E = \frac{2U}{R}$。
(3)离子在磁分析器中做匀速圆周运动，由题意可知，圆周运动的轨道半径为$d$，根据牛顿第二定律，有$qvB = m\frac{v^2}{d}$，
解得$B = \frac{1}{d}\sqrt{\frac{2mU}{q}}$。
设在$O_2T$上某点出射的离子的电荷量为$q'$，质量为$m'$，在磁场中运动的轨道半径为$r$，则在磁场中有$q'vB = \frac{m'v^2}{r}$，
在电场中有$q'E = \frac{m'v^2}{R}$，
解得$\frac{q'}{m'}=\frac{d^2}{r^2}·\frac{q}{m}$，
由此可知离子的比荷与运动半径的二次方成反比。
当离子运动半径最小时，比荷最大；当离子运动半径最大时，比荷最小。作出符合条件的离子的运动轨迹如图所示。

①在$O_2$处被检测到的离子的运动半径最小，离子的比荷最大，设此离子的运动半径为$r_1$，由几何关系可知$r_1 = \frac{1}{2}d$，
由$\frac{q_1}{m_1}=\frac{d^2}{r_1^2}·\frac{q}{m}$，
可得离子比荷的最大值为$k_1 = \frac{q_1}{m_1}=\frac{4q}{m}$；
②在$T$处被检测到的离子的运动半径最小，离子的比荷最大，设此离子的运动半径为$r_2$，由几何关系可知$(r_2 - d)^2 + (\sqrt{3}d)^2 = r_2^2$，
解得$r_2 = 2d$，
由$\frac{q_2}{m_2}=\frac{d^2}{r_2^2}·\frac{q}{m}$，
可得离子比荷的最小值为$k_2 = \frac{q_2}{m_2}=\frac{1}{4}·\frac{q}{m}=\frac{q}{4m}$。
因此，比荷$k$的范围为$\frac{q}{4m}\leq k\leq\frac{4q}{m}$。
答案
(1)$\sqrt{\frac{2qU}{m}}$
(2)$frac{2U}{R}$
(3)$\frac{q}{4m}\leq k\leq\frac{4q}{m}$