《2026年薪火金卷高考仿真模拟卷物理》

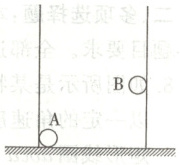
4. 放在水平地面上的光滑绝缘圆筒内有两个带正电的小球A、B，均可视为点电荷，A位于筒底靠在左侧壁处，B在右侧筒壁上受到A的斥力作用处于静止，如图所示。若A的电荷量保持不变，B由于漏电而下降少许重新平衡，下列说法正确的是
(A)

A.A对筒底的压力不变
B.B对筒壁的压力不变
C.A、B间的库仑力变小
D.A、B系统的电势能减小

答案：
4.A [对A、B系统由整体法可知，A对筒底的压力不变，故A正确；对球B受力分析如图所示：
　　　　　　
当B球下降时，$F_{库}$与水平方向的夹角$\alpha$变小，在竖直方向上有$F_{库} \sin \alpha =m_{B}g$，当$\alpha$变小时，$F_{库}$是变大的，而$F_{N}=F_{库} \cos \alpha$，显然$F_{N}$变大，故BC错误；因为B球下降后更靠近A球，克服库仑力做功，系统电势能增大，故D错误。]

5. 战绳是近几年比较流行的健身器材，两根相同的绳子一端固定，健身者双手握住另一端，上下抖动，形成“绳波”，“绳波”可以看作简谐横波。如图甲所示为一在绳上沿着x轴传播的简谐横波在$t = 1\ s$时的波形图，M、Q、P三个质点的平衡位置分别在x轴的2m、3.5m、4m处，图乙为P质点的振动图像，下列说法正确的是
(B)


A.波沿x轴负方向传播
B.从图甲时刻开始计时，Q经过$0.75\ s$第一次回到平衡位置
C.M点的振动方程为$y = 0.2\cos\pi t$
D.从$t = 1\ s$计时，再经$7\ s$，P质点的路程为$2.8\ m$

答案： 5.B [由同侧法可知，波沿$x$轴正方向传播，故A错误；结合波的传播方向，$Q$在$t=1\ s$时沿$y$轴正方向运动，波的传播速度$v=\dfrac{ \lambda }{T}=2\ m/s$，位于3 m处的波峰传到质点$Q$需要$\Delta t_{1}=\dfrac{ \Delta x}{v}=\dfrac{0.5\ m}{2\ m/s}=0.25\ s$，回到平衡位置需要$\dfrac{T}{4}=0.5\ s$，总时间为$t=0.25\ s+0.5\ s=0.75\ s$，故B正确；$M$质点比$P$质点超前$\pi$的相位，故$M$点的振动方程为$y=0.2 \sin \pi t$，故C错误；从$t=1\ s$计时，再经$7\ s$，即经过了$t=7\ s=3.5T$，$P$质点的路程为$s=3.5×4A=14A=2.8\ cm$，故D错误。故选B。]

6. 如图所示，有一均匀带正电的绝缘细圆环，半径为$r$、带电量为$q$。点P、Q、N把圆环进行三等分，现取走P、Q处两段弧长为$\Delta x$的小圆弧。NO延长线交细圆环于M，静电力常量为$k$，关于O点的电场强度
(A)


A.沿OM方向，大小为$\frac{kq\Delta x}{2\pi r^3}$
B.沿OM方向，大小为$\frac{kq\Delta x}{\pi r^3}$
C.沿ON方向，大小为$\frac{kq\Delta x}{2\pi^3}$
D.沿ON方向，大小为$\frac{kq\Delta x}{\pi^3}$

答案： 6.A [圆环所带电荷量均匀分布，故长度为$\Delta x$的小圆弧所带电荷量为$\Delta q=\dfrac{ \Delta x}{2 \pi r}q$，根据对称性，没有取走电荷时圆心$O$点的电场强度为零，取走$P$、$Q$两处的电荷后，圆环剩余电荷在$O$点产生的电场强度大小等于$P$、$Q$处弧长为$\Delta x$的小圆弧所带正电荷在$O$点产生的合电场强度的大小，方向相反，如图所示，可得$E_{剩}=E_{合}=2\dfrac{k \Delta q}{r^{2}} \cos 60^{ \circ }=\dfrac{kq \Delta x}{2 \pi r^{3}}$，$P$、$Q$两处在$O$点产生的合电场强度方向沿$ON$方向，取走$P$、$Q$后，$O$点的电场强度方向沿$OM$方向，故A正确。]

7. 如图所示，间距为$L$的倾斜光滑平行金属导轨的倾角$\theta = 30°$，底端接有阻值为$R$的定值电阻，虚线MN上方的导轨区域存在垂直于导轨平面向上的、范围足够大的匀强磁场，磁感应强度的大小为$B$，质量为$m$、阻值为$R$、长度为$L$的导体棒$ab$垂直于导轨放置。某时刻给$ab$一平行于导轨斜面向上的初速度，已知$ab$进入磁场时速度大小为$2v_0$，经过时间$t_0$速度减小为零，一段时间后，以大小为$v_0$的速度离开磁场。不计导轨的电阻，导体棒与导轨接触良好，且两者始终垂直，重力加速度为$g$。下列说法正确的是

(C)

A.导体棒在磁场中沿导轨上滑的最大距离为$\frac{4mv_0R - 2mg t_0 R}{B^2 L^2}$
B.导体棒在磁场中下滑过程中通过定值电阻的电荷量大小为$\frac{2mv_0 - mg t_0}{BL}$
C.导体棒在磁场中下滑过程经历的时间为$\frac{6v_0}{g} - t_0$
D.整个过程中定值电阻产生的焦耳热为$\frac{3}{2}mv_0$

答案： 7.C [导体棒上滑过程由动量定理得$mgt_{0} \sin \theta +B\overline{I}Lt_{0}=m×2v_{0}$，而$q=\overline{I}t_{0}=\dfrac{\overline{E}t_{0}}{2R}=\dfrac{ \Delta \varPhi }{2R}=\dfrac{BLx}{2R}$，联立解得$x=\dfrac{4mRv_{0}-mgRt_{0}}{B^{2}L^{2}}$，$q=\dfrac{4mv_{0}-mgl_{0}}{2BL}$，故A错误；下滑过程通过的距离$x$与上滑过程大小相等，因此电阻的电荷量大小与上滑过程的相等，故B错误；设导体棒在磁场中下滑过程经历的时间为$t_{1}$，此过程对导体棒有$mgt_{1} \sin \theta -BqL=mv_{0}$，解得$t_{1}=\dfrac{6v_{0}}{g}-t_{0}$，故C正确；整个过程中电路产生的总的焦耳热$Q_{总}=\dfrac{1}{2}m(2v_{0})^{2}-\dfrac{1}{2}mv^{2}_{0}$，定值电阻产生的焦耳热$Q_{R}=\dfrac{1}{2}Q_{总}=\dfrac{3}{4}mv^{2}_{0}$，故D错误。故选C。]