2026年薪火金卷高考仿真模拟卷物理
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年薪火金卷高考仿真模拟卷物理 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
10. 如图所示,足够长的光滑平行金属导轨间距为$L$,固定在竖直平面内,两根导轨上端用导线连接一个电容器,电容器的电容为$C$,导轨处于磁感应强度为$B$的匀强磁场中,磁场方向与导轨平面垂直。现将质量为$m$、长度也为$L$的金属棒$ab$紧贴导轨由静止释放,金属棒沿着导轨下滑过程中始终保持水平且与导轨接触良好,已知重力加速度为$g$,金属导轨和金属棒的电阻均不计。则当金属棒运动稳定后,有
(
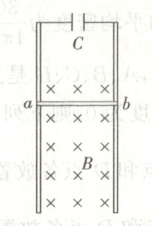
A.金属棒做匀加速运动,加速度大小为$\frac{mg}{m + CB^2 L^2}$
B.金属棒受到的安培力大小为$\frac{mCB^2 L^2}{m + CB^2 L^2}$
C.通过金属棒的电流大小为$\frac{CBLmg}{m + CB^2 L^2}$
D.电容器电荷量保持不变
(
AC
)
A.金属棒做匀加速运动,加速度大小为$\frac{mg}{m + CB^2 L^2}$
B.金属棒受到的安培力大小为$\frac{mCB^2 L^2}{m + CB^2 L^2}$
C.通过金属棒的电流大小为$\frac{CBLmg}{m + CB^2 L^2}$
D.电容器电荷量保持不变
答案:
10.AC[由题可知,金属棒$ab$受到的安培力为$F_{A}=BIL = B\frac{\Delta Q}{\Delta t}L$,又由动生电动势公式可知$Q = CU = CBLv$,所以电荷量的变化率$\frac{\Delta Q}{\Delta t}=\frac{CBL·\Delta v}{\Delta t}=CBLa$,所以安培力$F_{A}=CB^{2}L^{2}a$,对金属棒$ab$,由牛顿第二定律可得$mg - F_{A}=ma$,联立解得$a=\frac{mg}{m + CB^{2}L^{2}}$,由此可以看出,加速度恒定不变,所以金属棒$ab$做匀变速运动,故A正确;由以上过程可知,安培力大小$F_{A}=CB^{2}L^{2}a=\frac{mgCB^{2}L^{2}}{m + CB^{2}L^{2}}$,故B错误;根据安培力的计算可知,$BIL = CB^{2}L^{2}a$,变形后解得$I = CBLa = CBL\frac{mg}{m + CB^{2}L^{2}}$,故C正确;经过时间$t$电容器两端的电荷量为$q = CU = CBLv = CBLat=\frac{BCLmgt}{m + CB^{2}L^{2}}$,所以电容器的电荷量随时间逐渐增大,故D错误。]
11. (5分)某实验小组设计了如图所示装置,探究匀速圆周运动的物体所需要的向心力$F$与转动角速度$\omega$之间的关系。细线1上端固定在水平直杆并一直保持竖直状态,下端连接一个磁性小球(小球看作质点),竖直转轴上与磁性小球等高处固定另一个力传感器,用细线2连接力传感器和磁性小球,细线2伸直且水平,磁传感器固定在磁性小球附近,细线1、2的重力均不计,$\pi$取3.14。
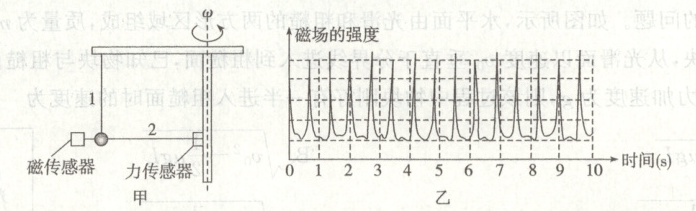
(1)用刻度尺测出细线1到转轴的距离$L$,将整个装置绕竖直转轴匀速转动,磁性小球每次经过磁传感器附近时磁传感器就接收到一个反映磁场强度的脉冲,如图乙所示。由图可知,磁性小球做圆周运动的周期$T=$
(2)多次改变转动的角速度$\omega$,获得多组对应的力传感器的示数$F$,为了直观地反映$F$与$\omega$的关系,以$F$为纵坐标,以

(1)用刻度尺测出细线1到转轴的距离$L$,将整个装置绕竖直转轴匀速转动,磁性小球每次经过磁传感器附近时磁传感器就接收到一个反映磁场强度的脉冲,如图乙所示。由图可知,磁性小球做圆周运动的周期$T=$
0.69(0.68~0.70)
s,做圆周运动的角速度为0.91(0.90~0.92)
$rad/s$。(结果均保留2位有效数字)(2)多次改变转动的角速度$\omega$,获得多组对应的力传感器的示数$F$,为了直观地反映$F$与$\omega$的关系,以$F$为纵坐标,以
ω²
(填“$\omega$”“$\frac{1}{\omega}$”“$\omega^2$”或“$\frac{1}{\omega^2}$”)为横坐标,在坐标纸中描点作图。如果得到一条过原点的倾斜直线,则表明小球质量和做圆周运动的半径一定时,向心力与角速度的平方成正比
;如果图像的斜率为$k$,则磁性小球的质量$m=$k/L
(用$L$和$k$表示)。
答案:
11.解析
(1)磁性小球做圆周运动的周期为$T=\frac{9.6}{14}s\approx0.69s$,做圆周运动的角速度为$\omega=\frac{2\pi}{T}\approx9.1rad/s$。
(2)根据$F = mr\omega^{2}$可知,为了直观地反映$F$与$\omega$的关系,以$F$为纵坐标,以$\omega^{2}$为横坐标;在坐标纸中描点作图,如果得到一条过原点的倾斜直线,则表明小球质量和做圆周运动的半径一定时,向心力与角速度的平方成正比;图像的斜率为$k = mL$,可知磁性小球的质量$m=\frac{k}{L}$。
答案
(1)$0.69(0.68~0.70)$ $0.91(0.90~0.92)$
(2)$\omega^{2}$ 小球质量和做圆周运动的半径一定时,向心力与角速度的平方成正比 $\frac{k}{L}$
(1)磁性小球做圆周运动的周期为$T=\frac{9.6}{14}s\approx0.69s$,做圆周运动的角速度为$\omega=\frac{2\pi}{T}\approx9.1rad/s$。
(2)根据$F = mr\omega^{2}$可知,为了直观地反映$F$与$\omega$的关系,以$F$为纵坐标,以$\omega^{2}$为横坐标;在坐标纸中描点作图,如果得到一条过原点的倾斜直线,则表明小球质量和做圆周运动的半径一定时,向心力与角速度的平方成正比;图像的斜率为$k = mL$,可知磁性小球的质量$m=\frac{k}{L}$。
答案
(1)$0.69(0.68~0.70)$ $0.91(0.90~0.92)$
(2)$\omega^{2}$ 小球质量和做圆周运动的半径一定时,向心力与角速度的平方成正比 $\frac{k}{L}$
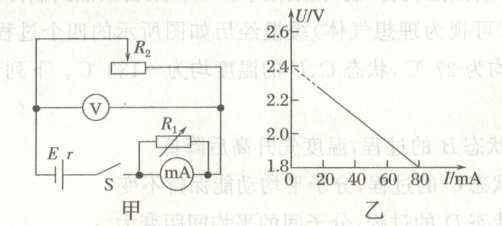
12. (10分)某同学从一个损坏的小台灯中拆出了一节锂电池,为了测量该锂电池的电动势,该同学设计了如图甲所示的电路,选用的器材如下:
A. 毫安表mA(量程为$100 mA$,内阻为$4\ \Omega$)
B. 电压表V(量程为$3 V$,内阻很大)
C. 电阻箱$R_1(0\sim 99.9\ \Omega)$
D. 滑动变阻器$R_2(0\sim 50\ \Omega)$
E. 待测锂电池(电动势标称值为$3.0 V$)
F. 开关一个、导线若干
(1)由于毫安表mA的量程太小,因此实验前需要将其改装成量程为$0.6 A$的电流表,图甲中电阻箱$R_1$应调整为
(2)改变滑动变阻器滑片的位置,记录两电表的示数,电压表的示数为$U$,毫安表的示数为$I$。
(3)描点得到如图乙所示的$U-I$图像,通过分析可知电源的电动势$E=$
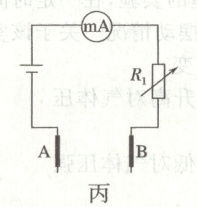
(4)用该锂电池、电阻箱$R_1$和量程为$100 mA$、内阻为$10\ \Omega$的毫安表改装成欧姆表,如图丙所示,表笔A是

A. 毫安表mA(量程为$100 mA$,内阻为$4\ \Omega$)
B. 电压表V(量程为$3 V$,内阻很大)
C. 电阻箱$R_1(0\sim 99.9\ \Omega)$
D. 滑动变阻器$R_2(0\sim 50\ \Omega)$
E. 待测锂电池(电动势标称值为$3.0 V$)
F. 开关一个、导线若干
(1)由于毫安表mA的量程太小,因此实验前需要将其改装成量程为$0.6 A$的电流表,图甲中电阻箱$R_1$应调整为
0.8
$\Omega$。(2)改变滑动变阻器滑片的位置,记录两电表的示数,电压表的示数为$U$,毫安表的示数为$I$。
(3)描点得到如图乙所示的$U-I$图像,通过分析可知电源的电动势$E=$
2.4
V,电源的内阻$r=$0.6
$\Omega$。(结果均保留1位小数)(4)用该锂电池、电阻箱$R_1$和量程为$100 mA$、内阻为$10\ \Omega$的毫安表改装成欧姆表,如图丙所示,表笔A是
红
(填“红”或“黑”)表笔,电阻箱应调至13.4
$\Omega$;正确使用该欧姆表测量某待测电阻$R_x$,毫安表指针指在$50 mA$处,则被测电阻$R_x$的阻值为24
$\Omega$。
答案:
12.解析
(1)根据串并联特点,改装后电流表的读数$I_{A}=I_{mA}+\frac{I_{mA}r_{mA}}{R_{1}}$,解得$R_{1}=0.8\Omega$,即题图甲中电阻箱$R_{1}$应调整为$0.8\Omega$。
(3)毫安表$mA$与电阻箱$R_{1}$并联后的电阻为$R_{A}=\frac{R_{1}r_{mA}}{R_{1}+r_{mA}}=\frac{2}{3}\Omega$,则根据闭合回路欧姆定律有$U = E - 6I(R_{A}+r)$,结合图像有$E = 2.4V$,$\frac{\Delta U}{\Delta I}=\frac{2.4 - 1.8}{0.08}\Omega=6(R_{A}+r)$,可得$r\approx0.6\Omega$。
(4)欧姆表中电流由红表笔流入,黑表笔流出,由题图丙可知,表笔$A$是红表笔;欧姆调零时,根据闭合回路欧姆定律有$I_{g}=\frac{E}{R_{A}'+R_{1}+r}$,解得$R_{1}=13.4\Omega$。由闭合回路欧姆定律有$I=\frac{E}{R_{A}'+R_{1}+r+R_{x}}$,解得$R_{x}=24\Omega$。
答案
(1)$0.8$
(3)$2.4$ $0.6$
(4)红 $13.4$ $24$
(1)根据串并联特点,改装后电流表的读数$I_{A}=I_{mA}+\frac{I_{mA}r_{mA}}{R_{1}}$,解得$R_{1}=0.8\Omega$,即题图甲中电阻箱$R_{1}$应调整为$0.8\Omega$。
(3)毫安表$mA$与电阻箱$R_{1}$并联后的电阻为$R_{A}=\frac{R_{1}r_{mA}}{R_{1}+r_{mA}}=\frac{2}{3}\Omega$,则根据闭合回路欧姆定律有$U = E - 6I(R_{A}+r)$,结合图像有$E = 2.4V$,$\frac{\Delta U}{\Delta I}=\frac{2.4 - 1.8}{0.08}\Omega=6(R_{A}+r)$,可得$r\approx0.6\Omega$。
(4)欧姆表中电流由红表笔流入,黑表笔流出,由题图丙可知,表笔$A$是红表笔;欧姆调零时,根据闭合回路欧姆定律有$I_{g}=\frac{E}{R_{A}'+R_{1}+r}$,解得$R_{1}=13.4\Omega$。由闭合回路欧姆定律有$I=\frac{E}{R_{A}'+R_{1}+r+R_{x}}$,解得$R_{x}=24\Omega$。
答案
(1)$0.8$
(3)$2.4$ $0.6$
(4)红 $13.4$ $24$
查看更多完整答案,请扫码查看


