2026年薪火金卷高考仿真模拟卷物理
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年薪火金卷高考仿真模拟卷物理 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
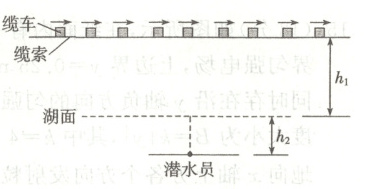
13. (10分)在一个平静的湖面上,距离水面高度$h_{1}=30\ \mathrm{m}$处缆车 缆索上每隔$t=10\ \mathrm{s}$就从站台以速度$v=$ 缆索
有一条水平缆索,缆索上每隔$t=10\ \mathrm{s}$就从站台以速度$v$沿一个方向持续开出一辆缆车。湖水深$h_{2}=8\ \mathrm{m}$,缆索中央正下方的湖底有一个潜水员,该潜水员只能看到湖面半径$r_{1}=9\ \mathrm{m}$的圆面有亮光,又在透过湖面半径$r_{2}=$ $6\ \mathrm{m}$的圆面上才能清晰的看到缆索上的缆车。已知$\sqrt{145}\approx12$,$\sin53^{\circ}=0.8$,$\cos53^{\circ}=0.6$,求:
(1)湖水的折射率$n$的大小(用分式表示);
(2)潜水员最多能清晰的看到缆索上缆车的数量。
有一条水平缆索,缆索上每隔$t=10\ \mathrm{s}$就从站台以速度$v$沿一个方向持续开出一辆缆车。湖水深$h_{2}=8\ \mathrm{m}$,缆索中央正下方的湖底有一个潜水员,该潜水员只能看到湖面半径$r_{1}=9\ \mathrm{m}$的圆面有亮光,又在透过湖面半径$r_{2}=$ $6\ \mathrm{m}$的圆面上才能清晰的看到缆索上的缆车。已知$\sqrt{145}\approx12$,$\sin53^{\circ}=0.8$,$\cos53^{\circ}=0.6$,求:
(1)湖水的折射率$n$的大小(用分式表示);
(2)潜水员最多能清晰的看到缆索上缆车的数量。

答案:
13. 解析
(1)根据题意可知,潜水员只能看到湖面半径$r_{1} = 9\ m$的圆面有亮光,如图所示,
则有$\sin C = \frac{r_{1}}{\sqrt{r_{1}^{2} + h_{2}^{2}}} = \frac{1}{n}$,
解得$n = \frac{4}{3}$。
(2)潜水员透过湖面半径$r_{2} = 6\ m$的圆面看到缆索,如图所示,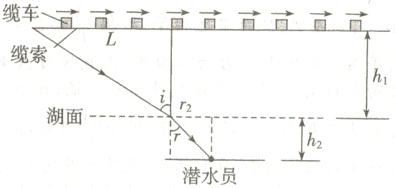
由几何关系有$\sin r = \frac{r_{2}}{\sqrt{r_{2}^{2} + h_{2}^{2}}}$,$\sin i = \frac{L}{\sqrt{L^{2} + h_{1}^{2}}}$,
又有$n = \frac{\sin i}{\sin r} = \frac{4}{3}$,
解得$L = 40\ m$。
由对称性可知,潜水员透过湖面半径$r_{2} = 6\ m$的圆面看到缆索的长度为$d = 2(L + r_{2}) = 92\ m$,
由题意可知,相邻缆车间的距离为$\Delta x = vt = 10\ m$,
则有$N = \frac{d}{\Delta x} = 9.2$,
即潜水员最多能清晰的看到缆索上缆车的数量为$10$。
答案
(1)$\frac{4}{3}$
(2)$10$
13. 解析
(1)根据题意可知,潜水员只能看到湖面半径$r_{1} = 9\ m$的圆面有亮光,如图所示,
则有$\sin C = \frac{r_{1}}{\sqrt{r_{1}^{2} + h_{2}^{2}}} = \frac{1}{n}$,
解得$n = \frac{4}{3}$。
(2)潜水员透过湖面半径$r_{2} = 6\ m$的圆面看到缆索,如图所示,

由几何关系有$\sin r = \frac{r_{2}}{\sqrt{r_{2}^{2} + h_{2}^{2}}}$,$\sin i = \frac{L}{\sqrt{L^{2} + h_{1}^{2}}}$,
又有$n = \frac{\sin i}{\sin r} = \frac{4}{3}$,
解得$L = 40\ m$。
由对称性可知,潜水员透过湖面半径$r_{2} = 6\ m$的圆面看到缆索的长度为$d = 2(L + r_{2}) = 92\ m$,
由题意可知,相邻缆车间的距离为$\Delta x = vt = 10\ m$,
则有$N = \frac{d}{\Delta x} = 9.2$,
即潜水员最多能清晰的看到缆索上缆车的数量为$10$。
答案
(1)$\frac{4}{3}$
(2)$10$
14. (14分)某同学在水平桌面上玩闯关游戏。在桌面最左端放置一质量$m_{\mathrm{A}}=0.1\ \mathrm{kg}$的小物体A(可视为质点),距离物体A为$s_{1}=1\ \mathrm{m}$处有一质量$m_{\mathrm{B}}=0.2\ \mathrm{kg}$的物体B(可视为质点),物体B距离桌面最右端为$s_{2}=2\ \mathrm{m}$,两物体在同一条直线上,如图所示。现使A以某一初速度沿直线向B运动,若A既能与B发生碰撞且碰后又不会滑离桌面,则闯关成功。已知A、B碰撞时间很短且碰后粘在一起,A、B两物体与桌面间的动摩擦因数均为$\mu=0.1$,重力加速度大小为$g=10\ \mathrm{m/s^{2}}$。为了确保闯关成功,求:

(1)物体A与B碰后的最大速度的大小$v_{\mathrm{m}}$;
(2)物体A与B碰撞过程损失机械能的最大值;
(3)物体A的初动能的范围。

(1)物体A与B碰后的最大速度的大小$v_{\mathrm{m}}$;
(2)物体A与B碰撞过程损失机械能的最大值;
(3)物体A的初动能的范围。
答案:
14. 解析
(1)若$A$、$B$碰后刚好不会滑离桌面,根据动能定理得$-\mu(m_{A} + m_{B})gs_{2} = 0 - \frac{1}{2}(m_{A} + m_{B})v_{m}^{2}$,
解得物体$A$与$B$碰后的最大速度的大小为$v_{m} = 2\ m/s$。
(2)若$A$、$B$碰后速度最大,则$A$、$B$碰撞过程损失的机械能最大,以向右为正方向,对$A$、$B$碰撞过程由动量守恒定律和能量守恒定律得$m_{A}v_{A} = (m_{A} + m_{B})v_{m}$,
$\frac{1}{2}m_{A}v_{A}^{2} = \frac{1}{2}(m_{A} + m_{B})v_{m}^{2} + E_{损}$,
解得物体$A$与$B$碰撞过程损失机械能的最大值为$E_{损} = 1.2\ J$。
(3)若$A$、$B$碰后速度最大,则碰前$A$的速度也为最大,初动能最大,$A$由桌面最左端到与$B$碰前瞬间,根据动能定理得$-\mu m_{A}gs_{1} = \frac{1}{2}m_{A}v_{A}^{2} - E_{kmax}$,
解得$E_{kmax} = 1.9\ J$;
若$A$与$B$碰前瞬间速度刚好减为零,则$A$的初动能最小,同理可得$-\mu m_{A}gs_{1} = 0 - E_{kmin}$,
解得$E_{kmin} = 0.1\ J$,
所以物体$A$的初动能的范围为$0.1\ J < E_{k} \leq 1.9\ J$。
答案
(1)$2\ m/s$
(2)$1.2\ J$
(3)$0.1\ J < E_{k} \leq 1.9\ J$
(1)若$A$、$B$碰后刚好不会滑离桌面,根据动能定理得$-\mu(m_{A} + m_{B})gs_{2} = 0 - \frac{1}{2}(m_{A} + m_{B})v_{m}^{2}$,
解得物体$A$与$B$碰后的最大速度的大小为$v_{m} = 2\ m/s$。
(2)若$A$、$B$碰后速度最大,则$A$、$B$碰撞过程损失的机械能最大,以向右为正方向,对$A$、$B$碰撞过程由动量守恒定律和能量守恒定律得$m_{A}v_{A} = (m_{A} + m_{B})v_{m}$,
$\frac{1}{2}m_{A}v_{A}^{2} = \frac{1}{2}(m_{A} + m_{B})v_{m}^{2} + E_{损}$,
解得物体$A$与$B$碰撞过程损失机械能的最大值为$E_{损} = 1.2\ J$。
(3)若$A$、$B$碰后速度最大,则碰前$A$的速度也为最大,初动能最大,$A$由桌面最左端到与$B$碰前瞬间,根据动能定理得$-\mu m_{A}gs_{1} = \frac{1}{2}m_{A}v_{A}^{2} - E_{kmax}$,
解得$E_{kmax} = 1.9\ J$;
若$A$与$B$碰前瞬间速度刚好减为零,则$A$的初动能最小,同理可得$-\mu m_{A}gs_{1} = 0 - E_{kmin}$,
解得$E_{kmin} = 0.1\ J$,
所以物体$A$的初动能的范围为$0.1\ J < E_{k} \leq 1.9\ J$。
答案
(1)$2\ m/s$
(2)$1.2\ J$
(3)$0.1\ J < E_{k} \leq 1.9\ J$
查看更多完整答案,请扫码查看


