2026年薪火金卷高考仿真模拟卷物理
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年薪火金卷高考仿真模拟卷物理 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
14. (14分)如图所示,在$xOy$平面第一象限内,直线$y = 0$与直线$y = x$之间存在磁感应强度大小为$B$,方向垂直于纸面向里的匀强磁场;$x$轴下方一直线$CD$与$x$轴平行且与$x$轴相距为$a$,密封$x$轴与直线$CD$之间(包含$x$轴)存在沿$y$轴正方向的匀强电场;在第三象限,直线$CD$与直线$EF$之间存在磁感应强度大小也为$B$、方向垂直于纸面向外的匀强磁场。纸面内有一束宽度为$a$的平行电子束如图,沿$y$轴负方向射入第一象限的匀强磁场,各电子的速度随入射位置不同大小各不相等,电子束的左边界与$y$轴的距离也为$a$,经第一象限的磁场偏转后发现所有电子都可以通过原点并进入$x$轴下方的电场,最后所有电子都垂直于$EF$边界离开磁场。其中电子质量为$m$,重力可忽略不计,电荷量大小为$e$,电场强度大小为$E = \frac{e a B^2}{2 m}$。求:
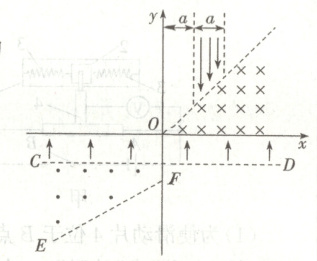
(1)各电子入射速度的范围;
(2)速度最小的电子在第三象限的磁场中做圆周运动的圆心的坐标;
(3)直线$EF$的方程。

(1)各电子入射速度的范围;
(2)速度最小的电子在第三象限的磁场中做圆周运动的圆心的坐标;
(3)直线$EF$的方程。
答案:
14.解析
(1)所有电子在第一象限都经历一个四分之一圆周运动后通过原点,并沿x轴负方向进入x轴下方的电场,故最大速度对应最大半径$r_{1} = 2a$,根据洛伦兹力提供向心力,则有$ev_{1}B = m\frac{v_{1}^{2}}{r_{1}}$,可得$v_{1} = \frac{2eBa}{m}$;同理,最小半径为$r_{2} = a$,可得最小速度为$v_{2} = \frac{eBa}{m}$,故入射速度范围为$\frac{eBa}{m}\leqslant v\leqslant \frac{2eBa}{m}$。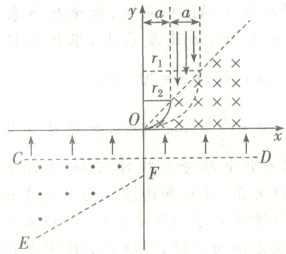
(2)所有电子在电场中做类平抛运动,水平方向有$x_{2} = v_{2}t$,竖直方向有$v_{y}^{2} = 2\frac{eE}{m}a$,$v_{min} = \sqrt{v_{2}^{2} + v_{y}^{2}}$,解得$v_{min} = \frac{\sqrt{2}eBa}{m}$,$x_{2} = 2a$;此后在磁场中的运动半径为$r_{3}$,则$ev_{min}B = m\frac{v_{min}^{2}}{r_{3}}$,解得$r_{3} = \sqrt{2}a$,电子射出CD时速度与竖直方向的夹角为$\tan\theta = \frac{v_{2}}{v_{y}}$,解得$\theta = 45^{\circ}$,设电子此后在磁场中运动的圆心为$(x,y)$,则$y = -a + (-r_{3}\sin 45^{\circ}) = -2a$,$x = -2a + r_{3}\cos 45^{\circ} = -a$,即该电子此后在磁场中运动的圆心坐标为$(-a, -2a)$。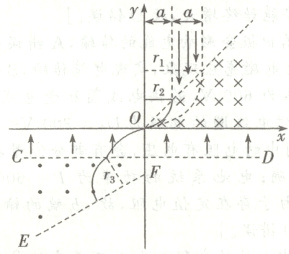
(3)所有电子都垂直于EF边界离开磁场,则所有电子运动轨迹的圆心都在EF直线上,由以上分析,经过直线CD时,不妨设任何电子的x轴负方向的分速度为$v_{x}' = k\frac{eBa}{m}(1\leqslant k\leqslant 2)$,则电子经过直线CD的合速度为$v_{合} = \sqrt{1 + k^{2}}\frac{eBa}{m}$,电子经过直线CD的坐标为$(-2ka, -a)$,速度方向与水平方向的夹角的正切值为$\tan\alpha = \frac{1}{k}$,则圆心位置为$(-2ka + a, -a - ka)$;因为电子垂直于直线EF出射,所以圆心也在直线上,可得EF直线为$y = \frac{1}{2}x - \frac{3}{2}a$。
答案
(1)$\frac{eBa}{m}\leqslant v\leqslant \frac{2eBa}{m}$
(2)$(-a, -2a)$
(3)$y = \frac{1}{2}x - \frac{3}{2}a$
14.解析
(1)所有电子在第一象限都经历一个四分之一圆周运动后通过原点,并沿x轴负方向进入x轴下方的电场,故最大速度对应最大半径$r_{1} = 2a$,根据洛伦兹力提供向心力,则有$ev_{1}B = m\frac{v_{1}^{2}}{r_{1}}$,可得$v_{1} = \frac{2eBa}{m}$;同理,最小半径为$r_{2} = a$,可得最小速度为$v_{2} = \frac{eBa}{m}$,故入射速度范围为$\frac{eBa}{m}\leqslant v\leqslant \frac{2eBa}{m}$。

(2)所有电子在电场中做类平抛运动,水平方向有$x_{2} = v_{2}t$,竖直方向有$v_{y}^{2} = 2\frac{eE}{m}a$,$v_{min} = \sqrt{v_{2}^{2} + v_{y}^{2}}$,解得$v_{min} = \frac{\sqrt{2}eBa}{m}$,$x_{2} = 2a$;此后在磁场中的运动半径为$r_{3}$,则$ev_{min}B = m\frac{v_{min}^{2}}{r_{3}}$,解得$r_{3} = \sqrt{2}a$,电子射出CD时速度与竖直方向的夹角为$\tan\theta = \frac{v_{2}}{v_{y}}$,解得$\theta = 45^{\circ}$,设电子此后在磁场中运动的圆心为$(x,y)$,则$y = -a + (-r_{3}\sin 45^{\circ}) = -2a$,$x = -2a + r_{3}\cos 45^{\circ} = -a$,即该电子此后在磁场中运动的圆心坐标为$(-a, -2a)$。

(3)所有电子都垂直于EF边界离开磁场,则所有电子运动轨迹的圆心都在EF直线上,由以上分析,经过直线CD时,不妨设任何电子的x轴负方向的分速度为$v_{x}' = k\frac{eBa}{m}(1\leqslant k\leqslant 2)$,则电子经过直线CD的合速度为$v_{合} = \sqrt{1 + k^{2}}\frac{eBa}{m}$,电子经过直线CD的坐标为$(-2ka, -a)$,速度方向与水平方向的夹角的正切值为$\tan\alpha = \frac{1}{k}$,则圆心位置为$(-2ka + a, -a - ka)$;因为电子垂直于直线EF出射,所以圆心也在直线上,可得EF直线为$y = \frac{1}{2}x - \frac{3}{2}a$。
答案
(1)$\frac{eBa}{m}\leqslant v\leqslant \frac{2eBa}{m}$
(2)$(-a, -2a)$
(3)$y = \frac{1}{2}x - \frac{3}{2}a$
15. (19分)如图所示,$L_3 = 1.5 m$的水平传送带顺时针匀速转动,紧靠传送带右端$C$处放置一个静止物块$c$,在距$c$处$L_4 = 0.25 m$的$D$处放置一竖直固定弹性挡板,物块$c$与挡板碰撞后会被原速率弹回;在距传送带左端$B$点$L_2 = 3 m$的$A$处放置物块$b$,$A$在$O$点的正下方,$A、B、C、D$在同一水平面上;物块$a$用长$L_1 = \frac{9}{8} m$的轻绳悬于$O$点,$OA = \frac{9}{8} m$。
现将物块$a$从偏离竖直方向$53°$角处由静止释放,一段时间后物块$a$与物块$b$发生弹性碰撞,碰撞时间忽略不计,物块$b$通过$AB$后,滑上传送带。已知$m_a = 2 kg、m_b = 1 kg、m_c = 1 kg$,物块$b$与水平面$AB$间的动摩擦因数$\mu_1 = 0.2$,物块$b、c$与传送带间的动摩擦因数$\mu_2 = 0.2$,与传送带右侧水平面间的动摩擦因数$\mu_3 = 0.02$,物块间的碰撞都是弹性正碰,不计物块大小,重力加速度$g$取$10 m/s^2$,$\sin 53° = 0.8$,$\cos 53° = 0.6$。求:

(1)物块$a$与物块$b$相碰后瞬间物块$b$的速度大小;
(2)物块$b$与物块$c$第一次碰撞前,物块$b$在传送带上滑行过程中因摩擦产生的热量;
(3)整个过程中,物块$c$与挡板碰撞的次数。
现将物块$a$从偏离竖直方向$53°$角处由静止释放,一段时间后物块$a$与物块$b$发生弹性碰撞,碰撞时间忽略不计,物块$b$通过$AB$后,滑上传送带。已知$m_a = 2 kg、m_b = 1 kg、m_c = 1 kg$,物块$b$与水平面$AB$间的动摩擦因数$\mu_1 = 0.2$,物块$b、c$与传送带间的动摩擦因数$\mu_2 = 0.2$,与传送带右侧水平面间的动摩擦因数$\mu_3 = 0.02$,物块间的碰撞都是弹性正碰,不计物块大小,重力加速度$g$取$10 m/s^2$,$\sin 53° = 0.8$,$\cos 53° = 0.6$。求:

(1)物块$a$与物块$b$相碰后瞬间物块$b$的速度大小;
(2)物块$b$与物块$c$第一次碰撞前,物块$b$在传送带上滑行过程中因摩擦产生的热量;
(3)整个过程中,物块$c$与挡板碰撞的次数。
答案:
15.解析:
(1)对物块a,从静止释放至运动到最低点的过程,由机械能守恒定律得$m_{a}g(L_{1} - L_{1}\cos 53^{\circ}) = \frac{1}{2}m_{a}v_{a}^{2}$,代入数据解得$v_{a} = 3m/s$。a、b两物块发生弹性碰撞,设碰后瞬间a的速度大小为$v_{a1}$,b的速度大小为$v_{b}$,规定向右为正方向,则有$m_{a}v_{a} = m_{a}v_{a1} + m_{b}v_{b}$,$\frac{1}{2}m_{a}v_{a}^{2} = \frac{1}{2}m_{a}v_{a1}^{2} + \frac{1}{2}m_{b}v_{b}^{2}$,代入数据解得$v_{a1} = 1m/s$,$v_{b} = 4m/s$。
(2)设物块b到达B点的速度大小为$v_{b1}$,由动能定理得$-\mu_{1}m_{b}gL_{2} = \frac{1}{2}m_{b}v_{b1}^{2} - \frac{1}{2}m_{b}v_{b}^{2}$,代入数据解得$v_{b1} = 2m/s$。物块b刚滑上传送带时速度大于传送带速度,物块b做匀减速运动,对物块b有$\mu_{2}m_{b}g = m_{b}a_{b}$,解得$a_{b} = 2m/s^{2}$。设物块b经时间t的速度与传送带速度相等,向右运动的位移为x,则有$t = \frac{v_{b1} - v}{a_{b}} = 0.5s$,$x = \frac{v_{b1} + v}{2}t = 0.75m$,由于$x < L_{3}$,所以物块b与传送带速度相等后与传送带一起做匀速运动,物块b匀减速运动过程中传送带向右运动的位移$s = vt = 0.5m$,因此物块b与传送带间因摩擦而产生的热量$Q = \mu_{2}m_{b}g(x - s)$,代入数据解得$Q = 0.5J$。
(3)物块b与物块c在传送带右端发生弹性碰撞,由于b与c质量相等,所以每一次碰撞速度都发生交换,第一次碰撞后瞬间$v_{c} = 1m/s$,由此可知,以后每次b与c相碰,速度都发生交换且由分析可知物块b不会再从传送带左端滑出。物块b与物块c第一次碰撞后瞬间物块c的动能$E_{kc} = \frac{1}{2}m_{c}v_{c}^{2} = 0.5J$,物块c从传送带右端到与弹性挡板碰撞后返回传送带右端消耗的能量$\Delta E_{0} = \mu_{3}m_{c}g× 2L_{4} = 0.1J$,由于$E_{kc} = 5\Delta E_{0}$,所以物块c与弹性挡板的碰撞次数为5次。
答案
(1)4m/s
(2)0.5J
(3)5
(1)对物块a,从静止释放至运动到最低点的过程,由机械能守恒定律得$m_{a}g(L_{1} - L_{1}\cos 53^{\circ}) = \frac{1}{2}m_{a}v_{a}^{2}$,代入数据解得$v_{a} = 3m/s$。a、b两物块发生弹性碰撞,设碰后瞬间a的速度大小为$v_{a1}$,b的速度大小为$v_{b}$,规定向右为正方向,则有$m_{a}v_{a} = m_{a}v_{a1} + m_{b}v_{b}$,$\frac{1}{2}m_{a}v_{a}^{2} = \frac{1}{2}m_{a}v_{a1}^{2} + \frac{1}{2}m_{b}v_{b}^{2}$,代入数据解得$v_{a1} = 1m/s$,$v_{b} = 4m/s$。
(2)设物块b到达B点的速度大小为$v_{b1}$,由动能定理得$-\mu_{1}m_{b}gL_{2} = \frac{1}{2}m_{b}v_{b1}^{2} - \frac{1}{2}m_{b}v_{b}^{2}$,代入数据解得$v_{b1} = 2m/s$。物块b刚滑上传送带时速度大于传送带速度,物块b做匀减速运动,对物块b有$\mu_{2}m_{b}g = m_{b}a_{b}$,解得$a_{b} = 2m/s^{2}$。设物块b经时间t的速度与传送带速度相等,向右运动的位移为x,则有$t = \frac{v_{b1} - v}{a_{b}} = 0.5s$,$x = \frac{v_{b1} + v}{2}t = 0.75m$,由于$x < L_{3}$,所以物块b与传送带速度相等后与传送带一起做匀速运动,物块b匀减速运动过程中传送带向右运动的位移$s = vt = 0.5m$,因此物块b与传送带间因摩擦而产生的热量$Q = \mu_{2}m_{b}g(x - s)$,代入数据解得$Q = 0.5J$。
(3)物块b与物块c在传送带右端发生弹性碰撞,由于b与c质量相等,所以每一次碰撞速度都发生交换,第一次碰撞后瞬间$v_{c} = 1m/s$,由此可知,以后每次b与c相碰,速度都发生交换且由分析可知物块b不会再从传送带左端滑出。物块b与物块c第一次碰撞后瞬间物块c的动能$E_{kc} = \frac{1}{2}m_{c}v_{c}^{2} = 0.5J$,物块c从传送带右端到与弹性挡板碰撞后返回传送带右端消耗的能量$\Delta E_{0} = \mu_{3}m_{c}g× 2L_{4} = 0.1J$,由于$E_{kc} = 5\Delta E_{0}$,所以物块c与弹性挡板的碰撞次数为5次。
答案
(1)4m/s
(2)0.5J
(3)5
查看更多完整答案,请扫码查看


