2026年薪火金卷高考仿真模拟卷物理
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年薪火金卷高考仿真模拟卷物理 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
14. (14分)如图,有一个正方体空间$I(O_{1}a_{1}b_{1}c_{1} - O_{3}a_{3}b_{3}c_{3})$和一个长方体空间$II(O_{1}a_{1}b_{1}c_{1} - O_{2}a_{2}b_{2}c_{2})$相拼接。以$O_{1}$为坐标原点,建立如图的空间直角坐标系$O_{1} - xyz$。空间$I$内存在沿$z$轴负方向的匀强电场(图中未画出),空间$II$内存在沿$z$轴正方向的匀强磁场(图中未画出)。一质量为$m$、电荷量为$q$的带正电的粒子从$O_{3}c_{3}$边的中点$P$以初速度$v_{0}$沿$x$轴正方向射入空间$I$,恰好经过正方形$O_{1}a_{1}b_{1}c_{1}$的中心点$Q$,并最终从空间$II$的竖直棱飞出长方体区域。空间$I$的棱长为$4L$,不计粒子重力。求:
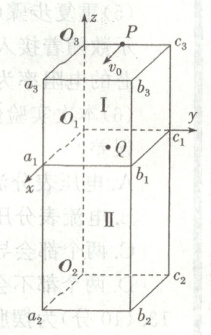
(1)匀强电场的电场强度大小;
(2)粒子经过$Q$点时的动能;
(3)匀强磁场的磁感应强度大小及长方体空间$II$竖直棱的最小高度。

(1)匀强电场的电场强度大小;
(2)粒子经过$Q$点时的动能;
(3)匀强磁场的磁感应强度大小及长方体空间$II$竖直棱的最小高度。
答案:
14.解析
(1)带正电粒子在空间Ⅰ中做类平抛运动,运动轨迹如图1所示
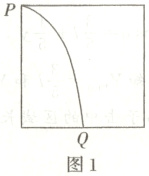
由平抛运动规律可得$2L=v_{0}t_{1}$,$4L=\frac{1}{2}at_{1}^{2}$,
由牛顿第二定律得$qE=ma$,
联立可得,匀强电场的电场强度大小为$E=\frac{2mv_{0}^{2}}{qL}$。
(2)在空间Ⅰ中,由动能定理得$qE×4L=E_{k}-\frac{1}{2}mv_{0}^{2}$,
解得粒子经过$Q$点时的动能为$E_{k}=\frac{17}{2}mv_{0}^{2}$。
(3)粒子进入空间Ⅱ时的速度大小为$v=\sqrt{\frac{2E_{k}}{m}}$,
解得$v=\sqrt{17}v_{0}$。
将速度$v$分解为沿$x$轴正方向的速度$v_{0}$和沿$z$轴负方向的速度$4v_{0}$,由于$z$轴速度方向与磁场平行,不产生洛伦兹力。在$xO_{1}y$平面内的分速度,使粒子受洛伦兹力,在$xO_{1}y$平面内做匀速圆周运动。故粒子要从竖直棱飞出,只能从棱$a_{1}a_{2}$飞出,其运动轨迹在$xO_{1}y$平面内的投影如图2所示
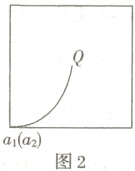
由洛伦兹力提供向心力,可得$qv_{0}B=m\frac{v_{0}^{2}}{r}$,
由几何关系可知$r=2L$,
可得匀强磁场的磁感应强度大小为$B=\frac{mv_{0}}{2qL}$。
运动时间$t=\frac{\frac{\pi r}{2}}{v_{0}}=\frac{\pi L}{v_{0}}$,
此段时间内,粒子不能脱离空间Ⅱ,故空间Ⅱ竖直棱的最小高度$H=4v_{0}t$,
解得$H=4\pi L$。
答案
(1)$\frac{2mv_{0}^{2}}{qL}$
(2)$\frac{17}{2}mv_{0}^{2}$
(3)$\frac{mv_{0}}{2qL}$ $4\pi L$
14.解析
(1)带正电粒子在空间Ⅰ中做类平抛运动,运动轨迹如图1所示

由平抛运动规律可得$2L=v_{0}t_{1}$,$4L=\frac{1}{2}at_{1}^{2}$,
由牛顿第二定律得$qE=ma$,
联立可得,匀强电场的电场强度大小为$E=\frac{2mv_{0}^{2}}{qL}$。
(2)在空间Ⅰ中,由动能定理得$qE×4L=E_{k}-\frac{1}{2}mv_{0}^{2}$,
解得粒子经过$Q$点时的动能为$E_{k}=\frac{17}{2}mv_{0}^{2}$。
(3)粒子进入空间Ⅱ时的速度大小为$v=\sqrt{\frac{2E_{k}}{m}}$,
解得$v=\sqrt{17}v_{0}$。
将速度$v$分解为沿$x$轴正方向的速度$v_{0}$和沿$z$轴负方向的速度$4v_{0}$,由于$z$轴速度方向与磁场平行,不产生洛伦兹力。在$xO_{1}y$平面内的分速度,使粒子受洛伦兹力,在$xO_{1}y$平面内做匀速圆周运动。故粒子要从竖直棱飞出,只能从棱$a_{1}a_{2}$飞出,其运动轨迹在$xO_{1}y$平面内的投影如图2所示

由洛伦兹力提供向心力,可得$qv_{0}B=m\frac{v_{0}^{2}}{r}$,
由几何关系可知$r=2L$,
可得匀强磁场的磁感应强度大小为$B=\frac{mv_{0}}{2qL}$。
运动时间$t=\frac{\frac{\pi r}{2}}{v_{0}}=\frac{\pi L}{v_{0}}$,
此段时间内,粒子不能脱离空间Ⅱ,故空间Ⅱ竖直棱的最小高度$H=4v_{0}t$,
解得$H=4\pi L$。
答案
(1)$\frac{2mv_{0}^{2}}{qL}$
(2)$\frac{17}{2}mv_{0}^{2}$
(3)$\frac{mv_{0}}{2qL}$ $4\pi L$
15. (18分)如图甲所示,在光滑水平地面上有质量分别为$m_{A} = 2\ kg$、$m_{B} = 1\ kg$的两小物块$A$、$B$,用细线连接并使中间的轻弹簧处于压缩状态(弹簧与两物块未拴接),弹簧的弹性势能为$E_{p} = 0.75\ J$。轴间距为$L_{1} = 4.5\ m$的水平传送带以$v = 4\ m/s$的速度顺时针匀速转动。传送带右侧放置一个倾角为$\theta = 30^{\circ}$的足够长的固定斜面,小物块$C$静止置于距斜面顶端$L_{2} = \frac{128}{15}\ m$处。现将$A$、$B$间的细线烧断,$B$与弹簧分离后冲上传送带,在传送带上运动后,从传送带右端水平飞出,恰好无碰撞地由斜面顶端滑入斜面,一段时间后$B$与$C$发生碰撞。$t = 0$时$B$、$C$恰完成第一次碰撞,$t = 2.4\ s$时刚要发生第二次碰撞,在$0 \sim 2.4\ s$内$B$运动的$v - t$图像如图乙所示(以沿斜面向下为正方向)。$B$、$C$每次碰撞均为弹性碰撞且碰撞时间极短,不计空气阻力,$B$与传送带间的动摩擦因数$\mu_{1} = 0.3$,物块$A$、$B$、$C$均可看作质点,重力加速度$g = 10\ m/s^{2}$,求:
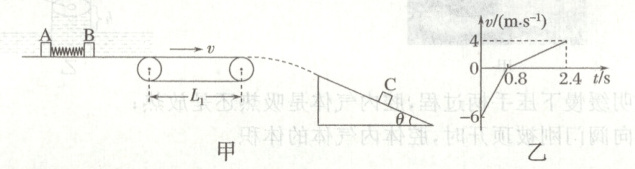
(1)$B$刚滑上传送带时的速度大小$v_{B}$;
(2)$C$的质量$m_{C}$以及$C$与斜面间的动摩擦因数$\mu_{2}$;
(3)$C$沿斜面下滑的最大距离$x_{m}$。

(1)$B$刚滑上传送带时的速度大小$v_{B}$;
(2)$C$的质量$m_{C}$以及$C$与斜面间的动摩擦因数$\mu_{2}$;
(3)$C$沿斜面下滑的最大距离$x_{m}$。
答案:
15.解析
(1)对$A、B$及弹簧系统,由动量及能量守恒定律得
$m_{B}v_{B}-m_{A}v_{A}=0$,$E_{p}=\frac{1}{2}m_{A}v_{A}^{2}+\frac{1}{2}m_{B}v_{B}^{2}$,
联立解得$v_{B}=1\ m/s$。
(2)若$B$在传送带上一直加速,由$\mu_{1}m_{B}g=m_{B}a_{1}$,得$a_{1}=3\ m/s^{2}$,由$v^{2}-v_{B}^{2}=2as$,得$s=2.5\ m<L_{1}$,
不合题意,故$B$在传送带上先做匀加速直线运动再做匀速直线运动。
$B$在斜面顶端有$v_{0}=\frac{v}{\cos\theta}$,
由$v-t$图像可知$B$每次在斜面上向上减速过程和向下加速过程的加速度大小分别为
$a_{2}=7.5\ m/s^{2}$,$a_{3}=2.5\ m/s^{2}$,
$B$在斜面上由顶端向下匀加速滑动过程中,有$v_{B1}^{2}-v_{0}^{2}=2a_{3}L_{2}$,
解得$v_{B1}=8\ m/s$;
对$B、C$第一次碰撞过程,有$m_{B}v_{B1}=m_{B}v_{B1}'+m_{C}v_{C1}$,
$\frac{1}{2}m_{B}v_{B1}^{2}=\frac{1}{2}m_{B}v_{B1}'^{2}+\frac{1}{2}m_{C}v_{C1}^{2}$,
解得$v_{C1}=2\ m/s$,$m_{C}=7\ kg$;
由$v-t$图像得$x_{1}=2.4\ m$,$x_{2}=3.2\ m$,
若$C$在经$x_{2}-x_{1}$过程后速度恰减为$0$,则由$\frac{v_{C1}+0}{2}t'=x_{2}-x_{1}$,
解得$t'=0.8\ s<2.4\ s$,
故$B$与$C$再次碰撞时$C$早已停止运动,
$B$与$C$第一次碰后,对$C$有
$0-v_{C1}^{2}=2(-a_{C})(x_{2}-x_{1})$,
$\mu_{2}m_{C}g\cos\theta-m_{C}g\sin\theta=m_{C}a_{C}$,
解得$\mu_{2}=\frac{\sqrt{3}}{2}$。
(3)设$B$第$n$次与$C$碰前的速度为$v_{Bn}$,由动量和能量守恒定律可知,碰后$B、C$的速度大小分别为$v_{Bn}'=\frac{3}{4}v_{Bn}$,$v_{Cn}=\frac{1}{4}v_{Bn}$,
第$n$次碰后$B$上升过程有$v_{Bn}'^{2}=2a_{2}x_{n}$,
$C$减速过程有$v_{Cn}^{2}=2a_{C}x_{Cn}$,
$B$与$C$第$(n+1)$次碰撞前的速度应满足$v_{B(n+1)}^{2}=2a_{3}(x_{n}+x_{Cn})$,
联立解得$v_{B(n+1)}=\frac{1}{2}v_{Bn}$,
则第$n$次碰撞后$C$的位移为$x_{Cn}=\frac{v_{Bn}^{2}}{32a_{C}}$,
第$(n+1)$次碰撞后$C$的位移为$x_{C(n+1)}=\frac{1}{4}×\frac{v_{Bn}^{2}}{32a_{C}}$,
又第一次碰后$C$的位移为$x_{C1}=0.8\ m$,
则每次碰后$C$的位移为$x_{Cn}=\frac{0.8}{4^{n-1}}\ m(n=1,2,3·s)$,
$C$沿斜面下滑的最大距离为$x_{m}=x_{1}+x_{2}+x_{3}+·s=\frac{0.8×\left[1-\left(\frac{1}{4}\right)^{n}\right]}{1-\frac{1}{4}}=\frac{16}{15}\ m$。
答案
(1)$1\ m/s$
(2)$7\ kg$ $\frac{\sqrt{3}}{2}$
(3)$\frac{16}{15}\ m$
(1)对$A、B$及弹簧系统,由动量及能量守恒定律得
$m_{B}v_{B}-m_{A}v_{A}=0$,$E_{p}=\frac{1}{2}m_{A}v_{A}^{2}+\frac{1}{2}m_{B}v_{B}^{2}$,
联立解得$v_{B}=1\ m/s$。
(2)若$B$在传送带上一直加速,由$\mu_{1}m_{B}g=m_{B}a_{1}$,得$a_{1}=3\ m/s^{2}$,由$v^{2}-v_{B}^{2}=2as$,得$s=2.5\ m<L_{1}$,
不合题意,故$B$在传送带上先做匀加速直线运动再做匀速直线运动。
$B$在斜面顶端有$v_{0}=\frac{v}{\cos\theta}$,
由$v-t$图像可知$B$每次在斜面上向上减速过程和向下加速过程的加速度大小分别为
$a_{2}=7.5\ m/s^{2}$,$a_{3}=2.5\ m/s^{2}$,
$B$在斜面上由顶端向下匀加速滑动过程中,有$v_{B1}^{2}-v_{0}^{2}=2a_{3}L_{2}$,
解得$v_{B1}=8\ m/s$;
对$B、C$第一次碰撞过程,有$m_{B}v_{B1}=m_{B}v_{B1}'+m_{C}v_{C1}$,
$\frac{1}{2}m_{B}v_{B1}^{2}=\frac{1}{2}m_{B}v_{B1}'^{2}+\frac{1}{2}m_{C}v_{C1}^{2}$,
解得$v_{C1}=2\ m/s$,$m_{C}=7\ kg$;
由$v-t$图像得$x_{1}=2.4\ m$,$x_{2}=3.2\ m$,
若$C$在经$x_{2}-x_{1}$过程后速度恰减为$0$,则由$\frac{v_{C1}+0}{2}t'=x_{2}-x_{1}$,
解得$t'=0.8\ s<2.4\ s$,
故$B$与$C$再次碰撞时$C$早已停止运动,
$B$与$C$第一次碰后,对$C$有
$0-v_{C1}^{2}=2(-a_{C})(x_{2}-x_{1})$,
$\mu_{2}m_{C}g\cos\theta-m_{C}g\sin\theta=m_{C}a_{C}$,
解得$\mu_{2}=\frac{\sqrt{3}}{2}$。
(3)设$B$第$n$次与$C$碰前的速度为$v_{Bn}$,由动量和能量守恒定律可知,碰后$B、C$的速度大小分别为$v_{Bn}'=\frac{3}{4}v_{Bn}$,$v_{Cn}=\frac{1}{4}v_{Bn}$,
第$n$次碰后$B$上升过程有$v_{Bn}'^{2}=2a_{2}x_{n}$,
$C$减速过程有$v_{Cn}^{2}=2a_{C}x_{Cn}$,
$B$与$C$第$(n+1)$次碰撞前的速度应满足$v_{B(n+1)}^{2}=2a_{3}(x_{n}+x_{Cn})$,
联立解得$v_{B(n+1)}=\frac{1}{2}v_{Bn}$,
则第$n$次碰撞后$C$的位移为$x_{Cn}=\frac{v_{Bn}^{2}}{32a_{C}}$,
第$(n+1)$次碰撞后$C$的位移为$x_{C(n+1)}=\frac{1}{4}×\frac{v_{Bn}^{2}}{32a_{C}}$,
又第一次碰后$C$的位移为$x_{C1}=0.8\ m$,
则每次碰后$C$的位移为$x_{Cn}=\frac{0.8}{4^{n-1}}\ m(n=1,2,3·s)$,
$C$沿斜面下滑的最大距离为$x_{m}=x_{1}+x_{2}+x_{3}+·s=\frac{0.8×\left[1-\left(\frac{1}{4}\right)^{n}\right]}{1-\frac{1}{4}}=\frac{16}{15}\ m$。
答案
(1)$1\ m/s$
(2)$7\ kg$ $\frac{\sqrt{3}}{2}$
(3)$\frac{16}{15}\ m$
查看更多完整答案,请扫码查看


