《2026年薪火金卷高考仿真模拟卷物理》

11. (5分)如图甲所示为某实验小组测量A、B两个箱子质量的装置图，其中D为铁架台，E为固定在铁架台上的轻质定滑轮(质量和摩擦可忽略)，F为光电门，C为固定在A上、宽度为$d$的细遮光条(质量不计)。此外该实验小组还准备了砝码一套(总质量$m_0 = 1\ kg$)和刻度尺等，请在以下实验步骤中按要求作答：

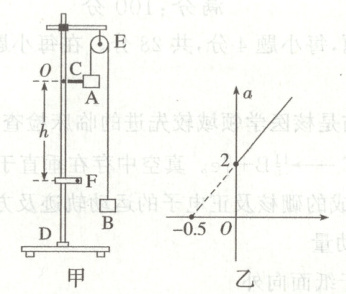
(1)在铁架台上标记一位置O，并测得该位置与光电门之间的高度差为$h$。
(2)取出质量为$m$的砝码放在A中，剩余砝码都放在B中，让A从位置O由静止开始下降。
(3)记录下遮光条通过光电门的时间$t$，根据所测数据计算出A下落到F处的速率$v =$$\dfrac{d}{t}$；下落过程中的加速度大小$a =$$\dfrac{d^{2}}{2ht^{2}}$。
(4)改变$m$，重复(2)(3)步骤，得到多组$m$及$a$的数据，作出$a-m$(填“$a - m$”或“$a - \frac{1}{m}$”)图像。
如图乙所示(图中横、纵坐标物理量的单位均采用国际制单位)。
(5)由图像可得，A的质量$m_A =$$3.0$$kg$，B的质量$m_B =$$1.0$$kg$(保留2位有效数字，重力加速度大小$g$取$10\ m/s^2$)。

答案： 11.解析
(3)由很短时间内的平均速度近似等于瞬时速度可知$v=\dfrac{d}{t}$；由匀变速直线运动的速度位移公式得$2ah=v^{2}=\dfrac{d^{2}}{t^{2}}$，解得$a=\dfrac{d^{2}}{2ht^{2}}$。
(4)由牛顿第二定律得$(m_{A}+m)g-\left \lbrack m_{B}+(m_{0}-m)g\right \rbrack=(m_{A}+m_{B}+m_{0})a$，解得$a=\dfrac{(m_{A}-m_{B}-m_{0})g+2mg}{m_{A}+m_{B}+m_{0}}$，所以应作出$a-m$图像。
(5) 图像斜率为$\dfrac{2g}{m_{A}+m_{B}+m_{0}}=4$，截距为$\dfrac{g(m_{A}-m_{B}-m_{0})}{m_{A}+m_{B}+m_{0}}=2$，联立解得$m_{A}=3.0\ kg$，$m_{B}=1.0\ kg$。
答案
(3)$\dfrac{d}{t}$ $\dfrac{d^{2}}{2ht^{2}}$
(4)$a-m$
(5)$3.0$ $1.0$

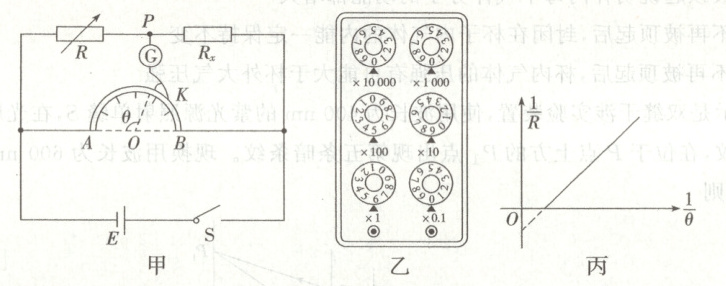
12. (10分)某物理兴趣小组的同学利用量角器、一段均匀电阻丝、电阻箱及灵敏电流计设计了一个测量电阻$R_x$的方案，实验电路如图甲所示。

①将电阻丝紧贴量角器圆弧边沿弯曲成型，并依量角器直径两端点裁剪好，通过导线接入电路；
②按图甲所示的电路原理图连接好各元件；
③将电阻箱的阻值调至$R_1$并使金属夹K从A端沿弧形电阻丝向B端移动，当灵敏电流计的示数为零时，停止移动金属夹，此时从量角器上读出OA、OK间的夹角$\theta_1$(单位为弧度)；
④改变电阻箱的阻值，重复步骤③，测得多组$(\theta, R)$值；
⑤整理数据并在坐标纸上描点绘图，所得图像如图丙所示。
根据分析，试回答下列问题：
(1)某次调节电阻箱的示数如图乙所示，则此时电阻箱接入电路的阻值为596.0$\Omega$。
(2)图像的斜率为$k$，由此可求得$R_x =$$\dfrac{ \pi }{k}$。
(3)实验时，当金属夹K调至某位置时，该小组的同学因为观察不仔细，认为灵敏电流计的读数已经为零，实际上，灵敏电流计还有从P到K的电流，那么此时测出$R_x$的值与真实值相比偏大(填“偏小”“相等”或“偏大”)。

答案： 12.解析
(1)由题图乙可知，电阻箱接入电路的阻值为$R=596.0\ \Omega$。
(2)当灵敏电流计的示数为零时，有$\dfrac{R}{R_{x}}=\dfrac{ \theta }{ \pi - \theta }$，
整理得$\dfrac{1}{R}=\dfrac{ \pi }{R_{x} \theta }-\dfrac{1}{R_{x}}$，
图像的斜率为$k=\dfrac{ \pi }{R_{x}}$，
解得$R_{x}=\dfrac{ \pi }{k}$。
(3)灵敏电流计还有从$P$到$K$的电流，则从量角器上读出$OA$、$OK$间的夹角$\theta$偏小，根据$R_{x}=\dfrac{ \pi - \theta }{ \theta }R$，此时测出$R_{x}$的值与真实值相比偏大。
答案
(1)$596.0$
(2)$\dfrac{ \pi }{k}$
(3)偏大