2026年薪火金卷高考仿真模拟卷物理
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年薪火金卷高考仿真模拟卷物理 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
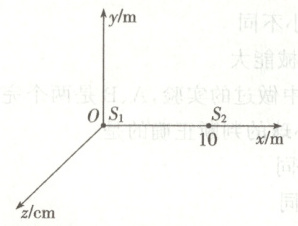
10. 如图所示,$x=0$与$x=10\ \mathrm{m}$处有两个波源$S_{1}$和$S_{2}$均可以沿$z$轴方向做简谐运动,两波源产生的机械波均能以波源为圆心在$xOy$平面内向各个方向传播,振动周期均为$T=2\ \mathrm{s}$,波速均为$v=1\ \mathrm{m/s}$。$t=0$时刻波源$S_{1}$开始沿$z$轴正方向振动,振幅$A_{1}=3\ \mathrm{cm}$;$t=2\ \mathrm{s}$时刻波源$S_{2}$开始沿$z$轴负方向振动,振幅$A_{2}=5\ \mathrm{cm}$。下列说法正确的是 (
A.$t=8\ \mathrm{s}$时刻,$x=5.5\ \mathrm{m}$处质点的位移为$z=-8\ \mathrm{cm}$
B.在$x$轴上,$x<0$和$x>10\ \mathrm{m}$区域都是振动的加强点
C.在$x$轴上,$0<x<10\ \mathrm{m}$区间内一共有10个振动的加强点
D.以波源$S_{1}$为圆心,分别以半径4.8 m和5.2 m画圆,则在这两个圆周上,振动的加强点的个数相等
CD
)
A.$t=8\ \mathrm{s}$时刻,$x=5.5\ \mathrm{m}$处质点的位移为$z=-8\ \mathrm{cm}$
B.在$x$轴上,$x<0$和$x>10\ \mathrm{m}$区域都是振动的加强点
C.在$x$轴上,$0<x<10\ \mathrm{m}$区间内一共有10个振动的加强点
D.以波源$S_{1}$为圆心,分别以半径4.8 m和5.2 m画圆,则在这两个圆周上,振动的加强点的个数相等
答案:
10. CD [假设只有波源$S_{1}$时,因波速$v = 1\ m/s$,此波传到$x = 5.5\ m$处需要的时间为$t_{1} = \frac{5.5}{1}\ s = 5.5\ s$,因周期$T = 2\ s$,则$x = 5.5\ m$处的质点又振动了$\Delta t = 8\ s - 5.5\ s = 2.5\ s = T + \frac{1}{4}T$,可知$x = 5.5\ m$处的质点在$t = 8\ s$时刻处在波峰,即位移是$3\ cm$,同理可知波源$S_{2}$存在时,传到$x = 5.5\ m$处需要的时间是$t_{2} = \frac{4.5}{1}\ s = 4.5\ s$,质点又振动了$\Delta t_{2} = 8\ s - 2\ s - 4.5\ s = 1.5\ s = \frac{3}{4}T$,即$x = 5.5\ m$处的质点在$t = 8\ s$时刻也处在波峰,则位移是$z = + 8\ cm$,A错误;该波的波长为$\lambda = vT = 1×2\ m = 2\ m$,在$x < 0$和$x > 10\ m$区域有,各点到两波源的距离之差$\Delta x = \frac{10}{2}\lambda = 5\lambda$,即是波长的整数倍,波源$S_{1}$和$S_{2}$的振动步调相反,因此各点都是振动减弱点,B错误;在$x$轴上,$0 < x < 10\ m$区间,中间位置是$O'$点,$O'$点左侧各点到两波源的距离之差$0 < \Delta x < 5\lambda$,因此$\Delta x = (2n + 1)\frac{\lambda}{2}$,即这样的加强点共有$5$个,分别为$n = 0$、$n = 1$、$n = 2$、$n = 3$、$n = 4$,同理,由对称性,$O'$右侧也有$5$个加强点,因此$0 < x < 10\ m$区间内一共有$10$个振动的加强点,C正确;以波源$S_{1}$为圆心,分别以半径$4.8\ m$和$5.2\ m$画圆,如图所示,则在这两个圆周上,$Q$点到两波源的距离之差最小,则有$\Delta x_{1} = 5.2\ m - 4.8\ m = 0.4\ m$,$Q'$点到两波源的距离之差最小$\Delta x_{1}' = 5.2\ m - 4.8\ m = 0.4\ m$,$P$点到两波源的距离之差最大为$\Delta x_{2} = 14.8\ m - 4.8\ m = 10\ m$,$P$点到两波源的距离之差最大为$\Delta x_{2}' = 15.2\ m - 5.2\ m = 10\ m$,则在这两个圆周上,振动的加强点的个数相等,D正确。]
10. CD [假设只有波源$S_{1}$时,因波速$v = 1\ m/s$,此波传到$x = 5.5\ m$处需要的时间为$t_{1} = \frac{5.5}{1}\ s = 5.5\ s$,因周期$T = 2\ s$,则$x = 5.5\ m$处的质点又振动了$\Delta t = 8\ s - 5.5\ s = 2.5\ s = T + \frac{1}{4}T$,可知$x = 5.5\ m$处的质点在$t = 8\ s$时刻处在波峰,即位移是$3\ cm$,同理可知波源$S_{2}$存在时,传到$x = 5.5\ m$处需要的时间是$t_{2} = \frac{4.5}{1}\ s = 4.5\ s$,质点又振动了$\Delta t_{2} = 8\ s - 2\ s - 4.5\ s = 1.5\ s = \frac{3}{4}T$,即$x = 5.5\ m$处的质点在$t = 8\ s$时刻也处在波峰,则位移是$z = + 8\ cm$,A错误;该波的波长为$\lambda = vT = 1×2\ m = 2\ m$,在$x < 0$和$x > 10\ m$区域有,各点到两波源的距离之差$\Delta x = \frac{10}{2}\lambda = 5\lambda$,即是波长的整数倍,波源$S_{1}$和$S_{2}$的振动步调相反,因此各点都是振动减弱点,B错误;在$x$轴上,$0 < x < 10\ m$区间,中间位置是$O'$点,$O'$点左侧各点到两波源的距离之差$0 < \Delta x < 5\lambda$,因此$\Delta x = (2n + 1)\frac{\lambda}{2}$,即这样的加强点共有$5$个,分别为$n = 0$、$n = 1$、$n = 2$、$n = 3$、$n = 4$,同理,由对称性,$O'$右侧也有$5$个加强点,因此$0 < x < 10\ m$区间内一共有$10$个振动的加强点,C正确;以波源$S_{1}$为圆心,分别以半径$4.8\ m$和$5.2\ m$画圆,如图所示,则在这两个圆周上,$Q$点到两波源的距离之差最小,则有$\Delta x_{1} = 5.2\ m - 4.8\ m = 0.4\ m$,$Q'$点到两波源的距离之差最小$\Delta x_{1}' = 5.2\ m - 4.8\ m = 0.4\ m$,$P$点到两波源的距离之差最大为$\Delta x_{2} = 14.8\ m - 4.8\ m = 10\ m$,$P$点到两波源的距离之差最大为$\Delta x_{2}' = 15.2\ m - 5.2\ m = 10\ m$,则在这两个圆周上,振动的加强点的个数相等,D正确。]

11. (5分)如图甲所示,某兴趣小组用单摆测量重力加速度。选用的实验器材有:智能手机、小球、细线、铁架台、夹子、游标卡尺、刻度尺等,实验操作如下:
①用铁夹将细线上端固定在铁架台上,将小球竖直悬挂;
②用刻度尺测出摆线的长度为$l$,用游标卡尺测出小球直径为$d$;
③将智能手机置于小球平衡位置的正下方,启用APP《手机物理工坊》的“近距秒表”功能;
④将小球由平衡位置拉开一个角度($\theta<5^{\circ}$),静止释放,软件同时描绘出小球与手机间距离随时间变化的图像,如图乙所示。
请回答下列问题:

(1)根据图乙可知,单摆的周期$T=$ $\mathrm{s}$。
(2)重力加速度$g$的表达式为
(3)改变摆线长度$l$,重复步骤②③④的操作,可以得到多组$T$和$l$的值,进一步描绘出如图丙的图像,则该图像以
①用铁夹将细线上端固定在铁架台上,将小球竖直悬挂;
②用刻度尺测出摆线的长度为$l$,用游标卡尺测出小球直径为$d$;
③将智能手机置于小球平衡位置的正下方,启用APP《手机物理工坊》的“近距秒表”功能;
④将小球由平衡位置拉开一个角度($\theta<5^{\circ}$),静止释放,软件同时描绘出小球与手机间距离随时间变化的图像,如图乙所示。
请回答下列问题:

(1)根据图乙可知,单摆的周期$T=$ $\mathrm{s}$。
2
(2)重力加速度$g$的表达式为
$\frac{4\pi^{2}}{T^{2}}\left(l + \frac{d}{2}\right)$
(用测得的物理量符号表示)。(3)改变摆线长度$l$,重复步骤②③④的操作,可以得到多组$T$和$l$的值,进一步描绘出如图丙的图像,则该图像以
$T^{2}$
(填“$\frac{1}{T}$”“$T$”或“$T^{2}$”)为横坐标;若图线的斜率为$k$,则重力加速度的测量值为$4\pi^{2}k$
。
答案:
11. 解析
(1)根据单摆的运动规律,一个周期内应该有两个小球与手机间距离的最小值,由题图乙可得出,单摆的周期为$T = 2\ s$。
(2)根据$T = 2\pi\sqrt{\frac{l + \frac{d}{2}}{g}}$,解得重力加速度的表达式为$g = \frac{4\pi^{2}}{T^{2}}\left(l + \frac{d}{2}\right)$。
(3)由
(2)问中重力加速度的表达式可得$l = \frac{g}{4\pi^{2}}T^{2} - \frac{d}{2}$,结合题图丙的图像可知,该图像以$T^{2}$为横坐标;
若图线的斜率为$k$,则$k = \frac{g}{4\pi^{2}}$,
可知重力加速度的测量值为$g = 4\pi^{2}k$。
答案
(1)$2$
(2)$\frac{4\pi^{2}}{T^{2}}\left(l + \frac{d}{2}\right)$
(3)$T^{2}$ $4\pi^{2}k$
(1)根据单摆的运动规律,一个周期内应该有两个小球与手机间距离的最小值,由题图乙可得出,单摆的周期为$T = 2\ s$。
(2)根据$T = 2\pi\sqrt{\frac{l + \frac{d}{2}}{g}}$,解得重力加速度的表达式为$g = \frac{4\pi^{2}}{T^{2}}\left(l + \frac{d}{2}\right)$。
(3)由
(2)问中重力加速度的表达式可得$l = \frac{g}{4\pi^{2}}T^{2} - \frac{d}{2}$,结合题图丙的图像可知,该图像以$T^{2}$为横坐标;
若图线的斜率为$k$,则$k = \frac{g}{4\pi^{2}}$,
可知重力加速度的测量值为$g = 4\pi^{2}k$。
答案
(1)$2$
(2)$\frac{4\pi^{2}}{T^{2}}\left(l + \frac{d}{2}\right)$
(3)$T^{2}$ $4\pi^{2}k$
查看更多完整答案,请扫码查看


