《2025年中学生数学课时精练八年级上册沪教版五四制》

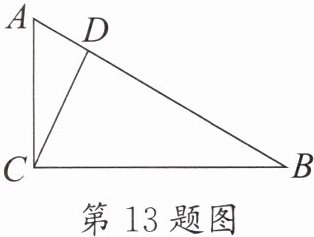
13. 已知：如图，在$Rt\triangle ABC$中，$\angle ACB = 90^{\circ}$，$CD\perp AB$，$AC = 12$，$BC:AB = 4:5$。
(1) 求$BC$、$AB$的长；
(2) 求$AD$的长。

答案：
(1) 设$BC = 4x$，$AB = 5x$，
由勾股定理在$Rt\triangle ABC$中，$AC^{2} + BC^{2} = AB^{2}$，
已知$AC = 12$，则$12^{2} + (4x)^{2} = (5x)^{2}$，
$144 + 16x^{2} = 25x^{2}$，
$9x^{2} = 144$，
$x^{2} = 16$，
因为$x\gt0$，所以$x = 4$。
所以$BC = 4×4 = 16$，$AB = 5×4 = 20$。
(2) 因为$CD\perp AB$，根据射影定理$AC^{2} = AD× AB$，
$12^{2} = AD×20$，
$144 = 20AD$，
$AD=\frac{144}{20} = 7.2$（或写为$\frac{36}{5}$）。
综上，BC长16，AB长20，AD长7.2（或$\frac{36}{5}$）。

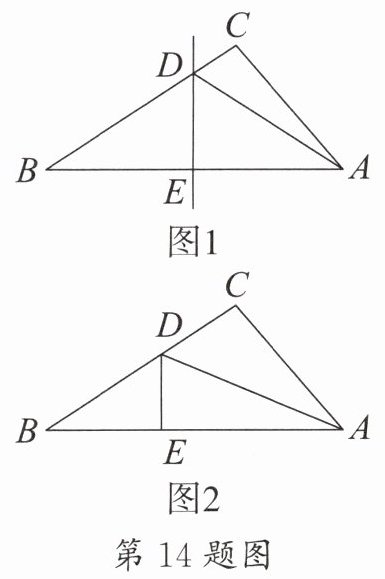
14. 已知：在$Rt\triangle ABC$中，$\angle C = 90^{\circ}$，进行如下操作：
(1) 如图$1$，将$Rt\triangle ABC$沿某条直线折叠，使斜边的两个端点$A$与$B$重合，折痕为$DE$，若$AC = 3$，$BC = 4$，求$CD$的长；
(2) 如图$2$，将直角边$AC$沿直线$AD$折叠，使它落在斜边$AB$上，且与$AE$重合，若$AC = 3$，$BC = 4$，求$CD$的长。

答案：
(1)$\frac{7}{8}$；
(2)$\frac{3}{2}$。

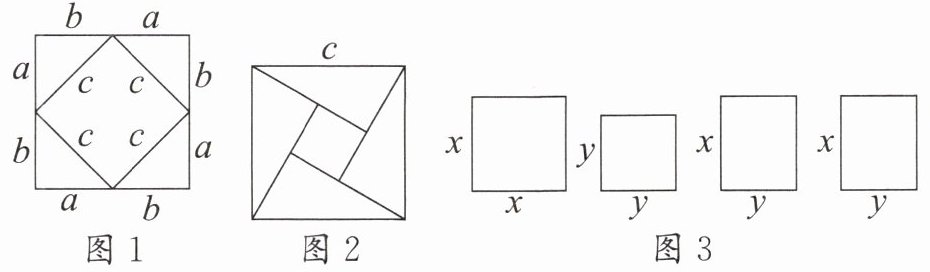
在学习勾股定理时，我们学会运用图$1$验证它的正确性. 图中大正方形的面积可表示为：$(a + b)^{2}$，也可表示为：$c^{2}+4(\frac{1}{2}ab)$，即$=(a + b)^{2}=c^{2}+4(\frac{1}{2}ab)$，由此推出勾股定理$a^{2}+b^{2}=c^{2}$，这种根据图形可以极简单地直观推论或验证数学规律和公式的方法，简称“无字证明”。
(1) 请你用图$2$（$2002$年国际数学家大会会标）的面积表达式验证勾股定理（其中四个直角三角形全等）；
(2) 请你用图$3$提供的图形进行组合，用组合图形的面积表达式验证：$(x + y)^{2}=x^{2}+2xy + y^{2}$。

(1)设直角三角形两直角边为$a$、$b$，斜边为$c$，中间小正方形边长为$(a - b)$。
大正方形面积$=c^{2}$，
又大正方形面积$=4×\frac{1}{2}ab+(a - b)^{2}=2ab+(a^{2}-2ab + b^{2})=a^{2}+b^{2}$，
故$a^{2}+b^{2}=c^{2}$。
(2)用边长为$x$的正方形、边长为$y$的正方形及2个长$x$宽$y$的长方形拼成边长为$(x + y)$的大正方形。
大正方形面积$=(x + y)^{2}$，
又大正方形面积$=x^{2}+y^{2}+xy + xy=x^{2}+2xy + y^{2}$，
故$(x + y)^{2}=x^{2}+2xy + y^{2}$。

答案：
(1)设直角三角形两直角边为$a$、$b$，斜边为$c$，中间小正方形边长为$(a - b)$。
大正方形面积$=c^{2}$，
又大正方形面积$=4×\frac{1}{2}ab+(a - b)^{2}=2ab+(a^{2}-2ab + b^{2})=a^{2}+b^{2}$，
故$a^{2}+b^{2}=c^{2}$。
(2)用边长为$x$的正方形、边长为$y$的正方形及2个长$x$宽$y$的长方形拼成边长为$(x + y)$的大正方形。
大正方形面积$=(x + y)^{2}$，
又大正方形面积$=x^{2}+y^{2}+xy + xy=x^{2}+2xy + y^{2}$，
故$(x + y)^{2}=x^{2}+2xy + y^{2}$。