《2025年中学生数学课时精练八年级上册沪教版五四制》

17. 已知$x = \dfrac{1}{\sqrt{3} - \sqrt{2}}$，$y = \dfrac{1}{\sqrt{3} + \sqrt{2}}$，求代数式$4x^{2} - 8xy + 4y^{2}$的值。

答案： 32

18. 化简求值：已知$a = \dfrac{1}{\sqrt{2} - 1}$，$b = \dfrac{1}{\sqrt{2} + 1}$，求$[\dfrac{a - b}{\sqrt{a} - \sqrt{b}} - (\sqrt{b} - \sqrt{a})] · (\sqrt{a} + \sqrt{b})$的值。

答案： 解题步骤：
1. 化简 $a$ 和 $b$
$a = \dfrac{1}{\sqrt{2} - 1} = \dfrac{\sqrt{2} + 1}{(\sqrt{2} - 1)(\sqrt{2} + 1)} = \sqrt{2} + 1$（分母有理化，平方差公式）
$b = \dfrac{1}{\sqrt{2} + 1} = \dfrac{\sqrt{2} - 1}{(\sqrt{2} + 1)(\sqrt{2} - 1)} = \sqrt{2} - 1$（分母有理化，平方差公式）
2. 化简原式中括号内部分
原式 = $\left[\dfrac{a - b}{\sqrt{a} - \sqrt{b}} - (\sqrt{b} - \sqrt{a})\right] · (\sqrt{a} + \sqrt{b})$
第一项：$\dfrac{a - b}{\sqrt{a} - \sqrt{b}} = \dfrac{(\sqrt{a} - \sqrt{b})(\sqrt{a} + \sqrt{b})}{\sqrt{a} - \sqrt{b}} = \sqrt{a} + \sqrt{b}$（平方差公式分解 $a - b$，约分化简）
第二项：$-(\sqrt{b} - \sqrt{a}) = \sqrt{a} - \sqrt{b}$（去括号）
中括号内合并：$(\sqrt{a} + \sqrt{b}) + (\sqrt{a} - \sqrt{b}) = 2\sqrt{a}$
3. 整体化简并代入计算
原式 = $2\sqrt{a} · (\sqrt{a} + \sqrt{b}) = 2(\sqrt{a} · \sqrt{a} + \sqrt{a} · \sqrt{b}) = 2(a + \sqrt{ab})$
计算 $ab$：$ab = (\sqrt{2} + 1)(\sqrt{2} - 1) = 1$（平方差公式）
代入 $a = \sqrt{2} + 1$，$\sqrt{ab} = 1$：
$2(a + \sqrt{ab}) = 2[(\sqrt{2} + 1) + 1] = 2(\sqrt{2} + 2) = 2\sqrt{2} + 4$
最终结论：$2\sqrt{2} + 4$

*19. 如图，某居民小区有块形状为长方形$ABCD$的绿地，长方形绿地的长$BC$为$\sqrt{243}$m，宽$AB$为$\sqrt{128}$m，现要在长方形绿地中修建一个长方形花坛(即图中阴影部分)，长方形花坛的长为$(\sqrt{14} + 1)$m、宽为$(\sqrt{14} - 1)$m。
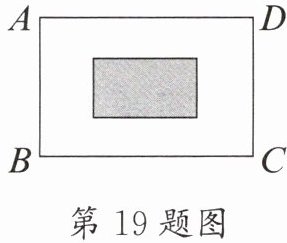
(1) 长方形$ABCD$的周长是多少？(结果化为最简二次根式)
(2) 除去修建花坛的地方，其他地方全修建成通道，通道上要铺上造价为$50$元$/m^{2}$的地砖，若要铺完整个通道，则购买地砖需要花费多少元？(结果化为最简二次根式)

答案：
(1) 长方形ABCD的长BC=√243=9√3 m，宽AB=√128=8√2 m，周长=2×(9√3 +8√2)=18√3 +16√2 m。
(2) 长方形ABCD面积=9√3×8√2=72√6 m²，花坛面积=(√14 +1)(√14 -1)=14 -1=13 m²，通道面积=72√6 -13 m²，花费=50×(72√6 -13)=3600√6 -650 元。
(1) 18√3 +16√2；
(2) 3600√6 -650。