《2025年基础训练大象出版社九年级数学全一册人教版》

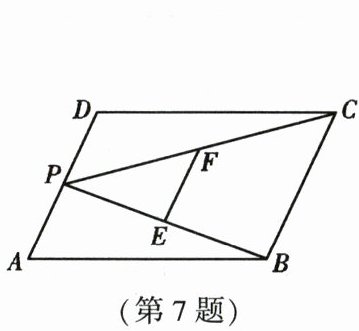
7. 如图,$P为□ ABCD的边AD$上的一点,$E$,$F分别为PB$,$PC$的中点,$\triangle PEF$,$\triangle PDC$,$\triangle PAB的面积分别为S$,$S_1$,$S_2$。若$S = 3$,则$S_1 + S_2$的值为(B)

A.24
B.12
C.6
D.3

答案： B

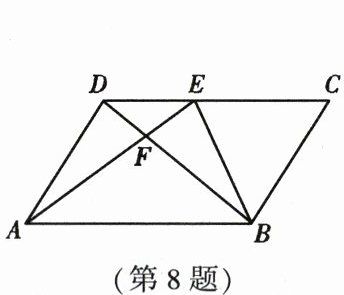
8. 如图,在$□ ABCD$中,$E为CD$上一点,连接$AE$,$BE$,$BD$,且$AE与BD交于点F$,$S_{\triangle DEF}:S_{\triangle ABF}= 4:25$,则$DE:EC$等于(A)

A.$2:3$
B.$2:5$
C.$3:5$
D.$3:2$

答案： A

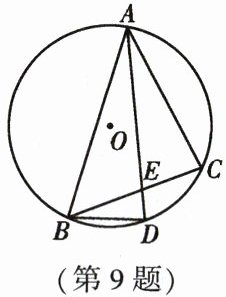
9. 如图,$\odot O是\triangle ABC$的外接圆,已知$AD平分\angle BAC交\odot O于点D$,交$BC边于点E$,$AD = 5$,$BD = 2$,则$DE$的长为(D)

A.$\frac{3}{5}$
B.$\frac{4}{25}$
C.$\frac{2}{25}$
D.$\frac{4}{5}$

答案： D

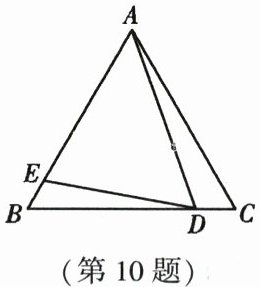
10. (2023·东营)如图,$\triangle ABC$为等边三角形,点$D$,$E分别在边BC$,$AB$上,$\angle ADE = 60^{\circ}$。若$BD = 4DC$,$DE = 2.4$,则$AD$的长为(C)

A.1.8
B.2.4
C.3
D.3.2

答案： C

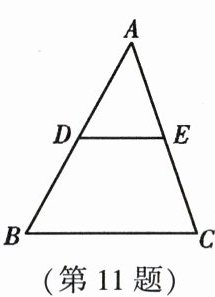
11. (2023·南通)如图,在$\triangle ABC$中,$D$,$E分别是AB$,$AC$的中点,连接$DE$,则$\frac{S_{\triangle ADE}}{S_{\triangle ABC}}= $$\frac{1}{4}$.

答案： $\frac{1}{4}$

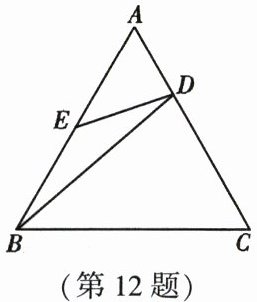
12. 如图,在等边三角形$ABC$中,点$D$,$E分别在AC$,$AB$上,且$\frac{AD}{AC}= \frac{1}{3}$,$AE = BE$,则与$\angle ADE$相等的角是$\angle CDB$.

答案： $\angle CDB$