《2025年基础训练大象出版社九年级数学全一册人教版》

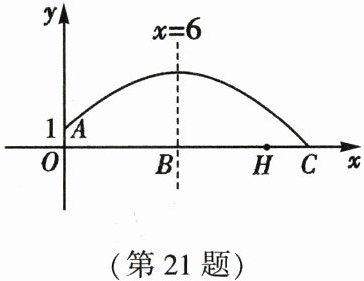
21. (10 分)(2023·安庆)如图,足球场上守门员徐杨在 $ O $ 处抛出一高球,球从离地面 1 m 处的点 $ A $ 飞出,其飞行的最大高度是 4 m,最高处距离飞出点的水平距离是 6 m,且飞行的路线是抛物线的一部分. 以点 $ O $ 为坐标原点,竖直向上的方向为 $ y $ 轴的正方向,球飞行的水平方向为 $ x $ 轴的正方向建立平面直角坐标系,并把球看成一个点.(参考数据：$ 4\sqrt{3} \approx 7 $)
(1)求足球的飞行高度 $ y $(单位：m)与飞行水平距离 $ x $(单位：m)之间的函数关系式.
(2)在没有队员干扰的情况下,球飞行的最远水平距离是多少？(精确到个位)
(3)若对方一名身高为 1.7 m 的队员在距落点 $ C $ 3 m 的点 $ H $ 处,跃起 0.3 m 进行拦截,则这名队员能拦到球吗？

答案：
(1)$y=-\frac{1}{12}(x-6)^2+4$；
(2)13m；
(3)不能。

22. (10 分)(2023·六安)我们定义两个不相交的函数图象在竖直方向上的最短距离为这两个函数的“和谐值”.
(1)求抛物线 $ y = x^{2} - 2x + 2 $ 与 $ x $ 轴的“和谐值”；
(2)求抛物线 $ y = x^{2} - 2x + 2 $ 与直线 $ y = x - 1 $ 的“和谐值”.

答案：
(1)
首先，对于抛物线$y = x^{2}-2x + 2=(x - 1)^{2}+1$，因为$(x - 1)^{2}\geqslant0$，所以$y=(x - 1)^{2}+1\geqslant1$，即抛物线在$x$轴上方，且与$x$轴无交点。
抛物线$y = x^{2}-2x + 2$与$x$轴（$y = 0$）在竖直方向上的距离为$d=(x^{2}-2x + 2)-0=(x - 1)^{2}+1$。
因为$(x - 1)^{2}\geqslant0$，所以当$x = 1$时，$d$取得最小值$1$。
所以抛物线$y = x^{2}-2x + 2$与$x$轴的“和谐值”为$1$。
(2)
设抛物线$y_{1}=x^{2}-2x + 2$，直线$y_{2}=x - 1$，则在竖直方向上的距离$d=y_{1}-y_{2}=x^{2}-2x + 2-(x - 1)=x^{2}-3x + 3$。
对于二次函数$d=x^{2}-3x + 3$，其中$a = 1$，$b=-3$，$c = 3$，根据顶点坐标公式$x=-\frac{b}{2a}$，可得$x=-\frac{-3}{2×1}=\frac{3}{2}$。
把$x = \frac{3}{2}$代入$d=x^{2}-3x + 3$，得$d=(\frac{3}{2})^{2}-3×\frac{3}{2}+3=\frac{9}{4}-\frac{9}{2}+3=\frac{9 - 18 + 12}{4}=\frac{3}{4}$。
所以抛物线$y = x^{2}-2x + 2$与直线$y = x - 1$的“和谐值”为$\frac{3}{4}$。