12. 在①线段、②平行四边形、③矩形、④菱形、⑤正方形、⑥正五边形、⑦正六边形、⑧圆这八种图形中,既是轴对称图形,又是中心对称图形的是
①③④⑤⑦⑧
. (只填序号)
答案:
①③④⑤⑦⑧
13. 如图,在平面直角坐标系中,点$B的坐标为(8,4)$,连接$OB$,将$OB绕点O逆时针旋转90^{\circ}$,得到$OB'$,则点$B'$的坐标为
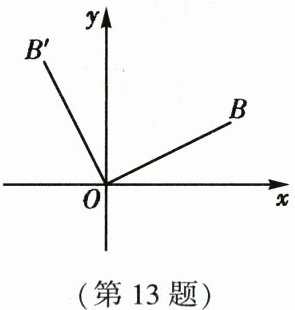
(-4,8)
.
答案:
(-4,8)
14. 如图,在$\triangle ABC$中,$AB = 4$,将$\triangle ABC绕点B按逆时针方向旋转45^{\circ}后得到\triangle A'BC'$,则阴影部分的面积为
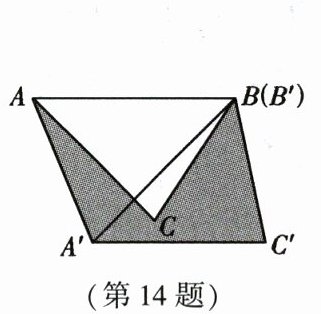
2π
.
答案:
2π
15. 如图,等边三角形$ABC$中,点$O是\triangle ABC$的中心,$\angle FOG = 120^{\circ}$,绕点$O旋转\angle FOG$,分别交线段$AB$,$BC于D$,$E$两点,连接$DE$. 给出下列四个结论:①$OD = OE$;②$S_{\triangle ODE} = S_{\triangle BDE}$;③四边形$ODBE$的面积始终等于定值;④当$OE\perp BC$时,$\triangle BDE$的周长最小. 其中正确的有
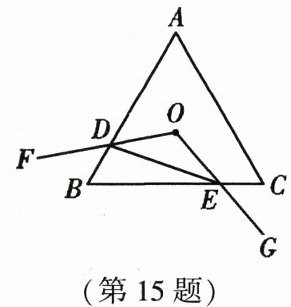
①③④
. (只填序号)
答案:
①③④
16. (5 分)如图,$\triangle ABC和\triangle DEF$是成中心对称的两个三角形,请找出它们的对称中心.
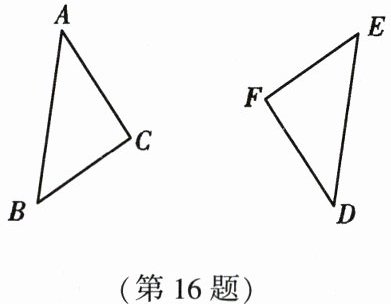

答案:
连接AD,连接CF,AD与CF交于点O,则点O即为对称中心。
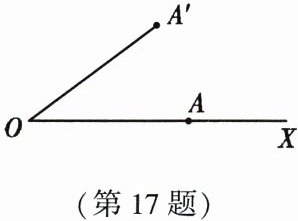
17. (10 分)(2022·常州)如图,点$A在射线OX$上,$OA = a$. 如果$OA绕点O按逆时针方向旋转n^{\circ}(0 < n\leqslant 360)到OA'$,那么点$A'的位置可以用(a,n^{\circ})$表示.
(1)按上述表示方法,若$a = 3$,$n = 37$,则点$A'$的位置可以表示为
(2)在(1)的条件下,已知点$B的位置用(3,74^{\circ})$表示,连接$AA'$,$A'B$,求证:$AA' = A'B$.
(1)按上述表示方法,若$a = 3$,$n = 37$,则点$A'$的位置可以表示为
$(3,37^{\circ})$
;
(2)在(1)的条件下,已知点$B的位置用(3,74^{\circ})$表示,连接$AA'$,$A'B$,求证:$AA' = A'B$.
证明:
因为点$A$位置为$(3,0^{\circ})$,点$A'$位置为$(3,37^{\circ})$,点$B$位置为$(3,74^{\circ})$,
所以$OA = OA'=OB = 3$,
$\angle AOA'=37^{\circ}$,$\angle A'OB = 74^{\circ}- 37^{\circ}=37^{\circ}$,
所以$\angle AOA'=\angle A'OB$,
在$\triangle AOA'$和$\triangle A'OB$中,
$\begin{cases}OA = OB\\\angle AOA'=\angle A'OB\\OA'=OA'\end{cases}$
根据$SAS$(边角边)定理,
可得$\triangle AOA'\cong\triangle A'OB$,
所以$AA' = A'B$。
因为点$A$位置为$(3,0^{\circ})$,点$A'$位置为$(3,37^{\circ})$,点$B$位置为$(3,74^{\circ})$,
所以$OA = OA'=OB = 3$,
$\angle AOA'=37^{\circ}$,$\angle A'OB = 74^{\circ}- 37^{\circ}=37^{\circ}$,
所以$\angle AOA'=\angle A'OB$,
在$\triangle AOA'$和$\triangle A'OB$中,
$\begin{cases}OA = OB\\\angle AOA'=\angle A'OB\\OA'=OA'\end{cases}$
根据$SAS$(边角边)定理,
可得$\triangle AOA'\cong\triangle A'OB$,
所以$AA' = A'B$。
答案:
(1) $(3,37^{\circ})$
(2)
证明:
因为点$A$位置为$(3,0^{\circ})$,点$A'$位置为$(3,37^{\circ})$,点$B$位置为$(3,74^{\circ})$,
所以$OA = OA'=OB = 3$,
$\angle AOA'=37^{\circ}$,$\angle A'OB = 74^{\circ}- 37^{\circ}=37^{\circ}$,
所以$\angle AOA'=\angle A'OB$,
在$\triangle AOA'$和$\triangle A'OB$中,
$\begin{cases}OA = OB\\\angle AOA'=\angle A'OB\\OA'=OA'\end{cases}$
根据$SAS$(边角边)定理,
可得$\triangle AOA'\cong\triangle A'OB$,
所以$AA' = A'B$。
(1) $(3,37^{\circ})$
(2)
证明:
因为点$A$位置为$(3,0^{\circ})$,点$A'$位置为$(3,37^{\circ})$,点$B$位置为$(3,74^{\circ})$,
所以$OA = OA'=OB = 3$,
$\angle AOA'=37^{\circ}$,$\angle A'OB = 74^{\circ}- 37^{\circ}=37^{\circ}$,
所以$\angle AOA'=\angle A'OB$,
在$\triangle AOA'$和$\triangle A'OB$中,
$\begin{cases}OA = OB\\\angle AOA'=\angle A'OB\\OA'=OA'\end{cases}$
根据$SAS$(边角边)定理,
可得$\triangle AOA'\cong\triangle A'OB$,
所以$AA' = A'B$。
查看更多完整答案,请扫码查看


