18. (9 分)(2023·周口模拟)如图,$AB是半圆O$的直径,$C$是半圆上一点(不与点$A$,$B$重合),连接$AC$,$BC$。$P为线段AB$延长线上一点,连接$PC$,$\angle CAB = \angle BCP$。
(1)求证:$PC为\odot O$的切线。
(2)作$\angle CPB$的平分线,交$AC于点M$,交$BC于点N$。
①请用无刻度的直尺和圆规完成作图(保留作图痕迹,不写作法);
②若$CN = 3$,求$MN$的长。
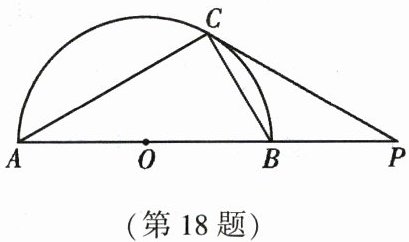
(1)求证:$PC为\odot O$的切线。
(2)作$\angle CPB$的平分线,交$AC于点M$,交$BC于点N$。
①请用无刻度的直尺和圆规完成作图(保留作图痕迹,不写作法);
②若$CN = 3$,求$MN$的长。

答案:
(1) 证明:
∵AB是半圆O的直径,
∴∠ACB=90°,
∴∠CAB+∠CBA=90°。
∵∠CAB=∠BCP,
∴∠BCP+∠CBA=90°。
∵OC=OB,
∴∠OCB=∠CBA,
∴∠BCP+∠OCB=90°,即∠OCP=90°。
∴OC⊥PC,故PC为⊙O的切线。
(2) ① 作图痕迹如图所示(作∠CPB的平分线,交AC于M,交BC于N)。
② 3√2
(1) 证明:
∵AB是半圆O的直径,
∴∠ACB=90°,
∴∠CAB+∠CBA=90°。
∵∠CAB=∠BCP,
∴∠BCP+∠CBA=90°。
∵OC=OB,
∴∠OCB=∠CBA,
∴∠BCP+∠OCB=90°,即∠OCP=90°。
∴OC⊥PC,故PC为⊙O的切线。
(2) ① 作图痕迹如图所示(作∠CPB的平分线,交AC于M,交BC于N)。
② 3√2
19. (9 分)(2023·武汉)如图,在$\triangle ABC$中,$AB = AC$,$D为AC$边上一点,$\odot I为\triangle ABD$的内切圆,$G$,$E$,$F$为切点。
(1)求证:$BE = CF$;
(2)若$BD = 10$,$CD = 4$,求$BE$的长。
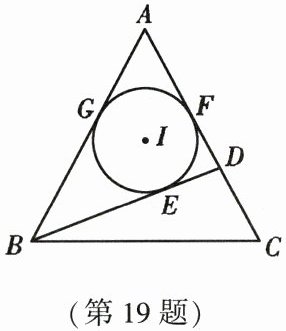
(1)求证:$BE = CF$;
(2)若$BD = 10$,$CD = 4$,求$BE$的长。

答案:
(1)见证明过程;
(2)$7$。
(1)见证明过程;
(2)$7$。
查看更多完整答案,请扫码查看


