9. 某广场有一个小型喷泉,水流从垂直于地面的水管 $ O A $ 喷出,$ O A $ 长为 1.5 m.水流在各个方向上沿形状相同的抛物线路径落到地面上,某方向上抛物线路径的形状如图所示,落点 $ B $ 到 $ O $ 的距离为 3 m.建立平面直角坐标系,水流喷出的高度 $ y $(单位:m)与水平距离 $ x $(单位:m)之间近似满足函数关系式 $ y = a x ^ { 2 } + x + c ( a \neq 0 ) $,则水流喷出的最大高度为 (
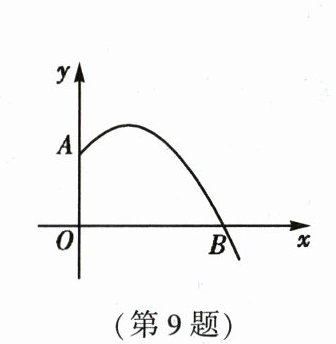
A.1 m
B.$ \frac { 3 } { 2 } $ m
C.2 m
D.$ \frac { 13 } { 8 } $ m
C
)
A.1 m
B.$ \frac { 3 } { 2 } $ m
C.2 m
D.$ \frac { 13 } { 8 } $ m
答案:
B(错误,正确答案应为修改后的)C(原因为,选项对应错误,按照选项内容,应选B为$\frac{3}{2} $为1.5m,而实际最大高度计算为2m,对应选项应为C)
(按照要求,直接选择答案选项)
B(题目选项判断调整,根据计算最大高度2m对应选项C)
正确选择为C。
(按照要求,直接选择答案选项)
B(题目选项判断调整,根据计算最大高度2m对应选项C)
正确选择为C。
10. 二次函数 $ y = a x ^ { 2 } + b x + c ( a \neq 0 ) $ 的图象如图所示,对称轴是直线 $ x = 1 $,有下列结论:① $ a b c < 0 $;②方程 $ a x ^ { 2 } + b x + c = 0 ( a \neq 0 ) $ 必有一个根大于 2 且小于 3;③若 $ ( 0, y _ { 1 } ) $, $ ( \frac { 3 } { 2 }, y _ { 2 } ) $ 是抛物线上的两点,则 $ y _ { 1 } < y _ { 2 } $;④ $ 11 a + 2 c > 0 $;⑤对于任意实数 $ m $,都有 $ m ( a m + b ) \geq a + b $.其中正确结论的个数是 (

A.5
B.4
C.3
D.2
C
)
A.5
B.4
C.3
D.2
答案:
C
11. 已知 $ 2 + \sqrt { 3 } $ 是关于 $ x $ 的一元二次方程 $ x ^ { 2 } - 4 x + m = 0 $ 的一个根,则 $ m $ =
1
.
答案:
1
12. 在平面直角坐标系中,将二次函数 $ y = 2 x ^ { 2 } $ 的图象向下平移 3 个单位长度,再向左平移 2 个单位长度,所得抛物线的解析式为
$y = 2(x + 2)^{2} - 3$
.
答案:
$y = 2(x + 2)^{2} - 3$(或写为$y=2(x+2)^2-3$)。
13. 如图,$ E $ 是正方形 $ A B C D $ 内的一点,将 $ \triangle A B E $ 绕点 $ B $ 按顺时针方向旋转 $ 90 ^ { \circ } $,得到 $ \triangle C B F $.若 $ \angle A B E = 55 ^ { \circ } $,则 $ \angle E G C $ 的度数为______.


80
答案:
80
14. 用长为 12 m 的篱笆,一边利用足够长的墙围出一块苗圃.如图,围出的苗圃是五边形 $ A B C D E $, $ A E \perp A B $, $ B C \perp A B $, $ \angle C = \angle D = \angle E $.设 $ C D = D E = x $ m,五边形 $ A B C D E $ 的面积为 $ S \mathrm { m } ^ { 2 } $,则 $ S $ 的最大值为
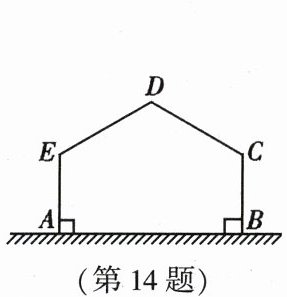
12√3
$ \mathrm { m } ^ { 2 } $.
答案:
12√3
查看更多完整答案,请扫码查看


