《2025年同步练习河南大学出版社八年级物理全一册沪科版》

9. 小雨家离图书馆 $2.5km$,他以 $5km/h$ 的速度步行前往图书馆,出发 $10min$ 后妈妈发现小雨的笔记本忘记带了,立即以 $15km/h$ 的速度沿小雨步行的方向骑车去追小雨,求：
(1) 小雨从家到图书馆需要花费多少分钟？
(2) 妈妈经过多少分钟能追上小雨？

答案：
(1)小雨从家到图书馆用时为:
$t_{1}=\frac{s}{v_{1}}=\frac{2.5\ km}{5\ km/h}=0.5\ h=30\ min$
(2)小雨出发10 min走过的路程为:
$s_{2}=v_{1}t_{2}=5\ km/h×\frac{10}{60}\ h=\frac{5}{6}\ km$
若妈妈追上小雨用时为$t_{3}$,则有:
$v_{2}t_{3}=v_{1}t_{3}+s_{2}$
代入数据得:
$t_{3}=\frac{s_{2}}{v_{2}-v_{1}}=\frac{\frac{5}{6}\ km}{15\ km/h-5\ km/h}=\frac{1}{12}\ h=5\ min$

10. 国庆节期间,小陆从遵义乘车去北京旅游,他乘坐的火车长为 $500m$。途中当火车以 $72km/h$ 的速度匀速穿过一条隧道时,小陆测出自己通过该隧道的时间为 $1min5s$。
(1) 该隧道的长度为多少米？
(2) 火车完全通过该隧道需要的时间为多少秒？
(3) 若该火车通过一座长为 $0.8km$ 的大桥时,火车完全在桥上的时间为 $12s$,则该火车过桥的平均速度为多少米每秒？

答案：
(1)由题意可知,火车速度为:
$v=72\ km/h=20\ m/s$
通过隧道的时间为:
$t=1\ min\ 5\ s=65\ s$
由$s=vt$可得,隧道长为:
$s_{隧道}=vt=20\ m/s×65\ s=1300\ m$
(2)火车完全通过隧道通过的路程:
$s_{1}=1300\ m+500\ m=1800\ m$
根据$v=\frac{s}{t}$可得,火车完全通过隧道的时间为:
$t_{1}=\frac{s_{1}}{v}=\frac{1800\ m}{20\ m/s}=90\ s$
(3)由题意可知,大桥的长度0.8 km=800 m,所以火车完全在桥上的路程为:
$s_{2}=800\ m-500\ m=300\ m$
火车完全在桥上的时间为12 s,所以火车过桥时的平均速度为:
$v_{2}=\frac{s_{2}}{t_{2}}=\frac{300\ m}{12\ s}=25\ m/s$

11. 汽车遇到紧急情况停车要经历反应和制动两个过程,汽车在反应过程中做匀速直线运动,在制动过程做变速直线运动,如图所示。某司机驾车前行时,突然发现前方 $65m$ 处有障碍物。司机从发现险情到刹车制动需要的反应时间为 $0.6s$,这段时间内汽车保持原速匀速前行了 $12m$。汽车制动后还要继续向前滑行 $21m$,用时 $2.4s$ 才能停下。求：

(1) 汽车制动前的速度是多少千米每小时？
(2) 汽车整个过程的平均速度是多少米每秒？
(3) 若司机酒后驾车,反应时间是平时的 $4$ 倍,请通过计算判断汽车是否会撞上障碍物。

答案：
(1)汽车制动前的速度:
$v_{制动前}=\frac{s_{制动前}}{t_{0}}=\frac{12\ m}{0.6\ s}=20\ m/s=72\ km/h$
(2)汽车整个过程的平均速度:
$v_{全}=\frac{s_{全}}{t}=\frac{12\ m+21\ m}{0.6\ s+2.4\ s}=11\ m/s$
(3)若司机酒后驾车,反应时间是平时的4倍,则反应时间为:
$t_{反}=4t_{0}=4×0.6\ s=2.4\ s$
则反应距离为:
$s=v_{制动前}t_{反}=20\ m/s×2.4\ s=48\ m$
汽车再向前滑行21 m,总路程为69 m,大于65 m,故会撞上障碍物。

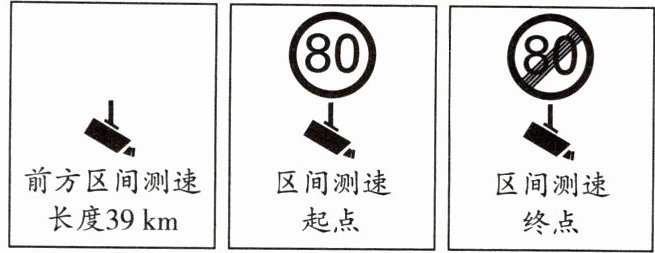
12. 为了有效遏制超速行为,保障高速公路上的行车安全,交通管理部门加大了道路限速监控管理力度,其中一种方式是采用“区间测速”。“区间测速”就是测算出汽车在某一区间内行驶的平均速度,如果超过了该区间的最高限速,即被判为超速。如图所示是某高速公路上的一个区间测速的相关标识,某汽车以 $70km/h$ 的速度进入该区间测速路段(全长为 $39km$),匀速行驶了一段距离后又以 $100km/h$ 的速度匀速行驶了 $15min$,然后再以 $70km/h$ 的速度继续匀速行驶直至离开该区间测速路段。
(1) 求汽车以 $100km/h$ 的速度行驶的路程。
(2) 请通过计算说明,该车通过该测速区间会不会被判超速。
(3) 在确保不会被判超速的情况下,该车通过该测速区间所需要的最少时间为多少？

答案：
(1)汽车以100 km/h的速度行驶的路程:
$s_{1}=v_{1}t_{1}=100\ km/h×\frac{15}{60}\ h=25\ km$
(2)以70 km/h的速度行驶的路程:
$s_{2}=s-s_{1}=39\ km-25\ km=14\ km$
以70 km/h的速度行驶的时间:
$t_{2}=\frac{s_{2}}{v_{2}}=\frac{14\ km}{70\ km/h}=0.2\ h$
此路段行驶的时间:
$t=t_{1}+t_{2}=\frac{15}{60}\ h+0.2\ h=0.45\ h$
平均速度:
$v=\frac{s}{t}=\frac{39\ km}{0.45\ h}\approx86.7\ km/h＞80\ km/h$
所以会被判超速。
(3)以最大速度$v_{大}'=80\ km/h$行驶所用时间最少,行驶的最少时间:
$t_{少}=\frac{s}{v_{大}}=\frac{39\ km}{80\ km/h}=0.4875\ h=29.25\ min$