《2025年名师面对面学科素养评价八年级数学上册浙教版》

7. 如图，$\triangle ABC\cong\triangle DCB$，$\angle DBC = 40^{\circ}$，则$\angle AEB =$80$^{\circ}$.

答案： 7.80

8. 如图，$A$，$D$，$E$三点在同一直线上，且$\triangle BAD\cong\triangle ACE$，$\angle BDA = 80^{\circ}$.
(1) 求$\angle E$和$\angle BAC$的度数.
(2) 求证：$BD = CE + DE$.

答案： 8.
(1)解：
∵△BAD≌△ACE,∠BDA=80°,
∴∠E=∠BDA=80°,∠ABD=∠CAE,
∴∠BAC=∠BAD+∠CAE=∠BAD+∠ABD=180°-
∠BDA=180°-80°=100°.
(2)证明：
∵△BAD≌△ACE,
∴BD=AE,AD=CE,
∴BD=AE=AD+DE=CE+DE,
即BD=DE+CE.

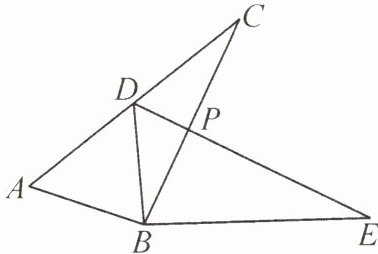
9. 如图，已知$\triangle ABC\cong\triangle DBE$，点$D$在$AC$上，$BC$与$DE$交于点$P$.
(1) 若$\angle ABE = 160^{\circ}$，$\angle DBC = 30^{\circ}$，求$\angle CBE$的度数.
(2) 若$AD = DC = 3\mathrm{cm}$，$BC = 4.5\mathrm{cm}$，求$\triangle DCP$与$\triangle BPE$的周长之和.

答案： 9.解：
(1)
∵△ABC≌△DBE,
∴∠ABC=∠DBE,
∴∠ABC-∠DBC=∠DBE-∠DBC,
即∠ABD=∠CBE=$\frac{1}{2}$(160°-30°)=65°.
(2)
∵△ABC≌△DBE,
∴BE=BC=4.5cm,DE=AC=6cm,
∴△DCP与△BPE的周长之和
=DC+DP+PC+BP+PE+BE
=(DP+PE)+(BP+PC)+DC+BE
=18cm.