《2025年名师面对面学科素养评价八年级数学上册浙教版》

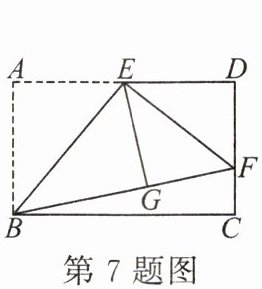
7. 如图，在长方形 $ABCD$ 中，$E$ 是 $AD$ 的中点，将 $\triangle ABE$ 沿直线 $BE$ 折叠后得到 $\triangle GBE$，延长 $BG$ 交 $CD$ 于点 $F$，连结 $EF$。若 $AB = 6$，$BC = 4\sqrt{6}$，则 $FD$ 的长为(B)

A.2
B.4
C.$\sqrt{6}$
D.$2\sqrt{3}$

答案： 7.B 【解析】可证△EDF ≌ △EGF,
∴DF = GF = x, 在△BCF 中$, (x + 6)^2 = (\sqrt{96})^2 + (6 - x)^2, $解得 x = 4.

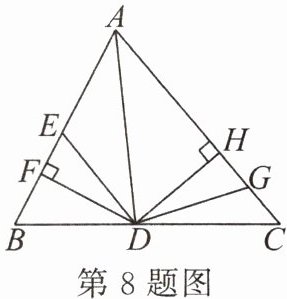
8. 如图，$D$ 是 $BC$ 上的一点，$DF\perp AB$，$DH\perp AC$，垂足分别为 $F$，$H$，且 $DF = DH$，$DE = DG$。若 $\triangle ADG$ 和 $\triangle AED$ 的面积分别为 10 和 6，则 $\triangle EDF$ 的面积为2。

答案： 8.2

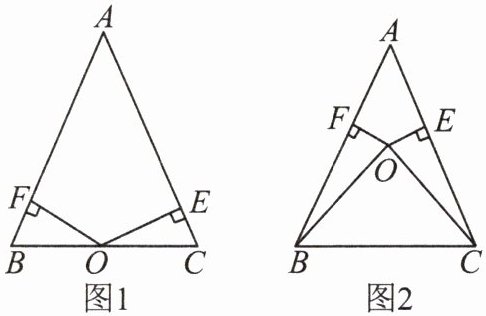
9. 已知：点 $O$ 到 $\triangle ABC$ 的两边 $AB$，$AC$ 所在直线的距离相等，且 $OB = OC$。
（1）如图 1 所示，点 $O$ 在 $BC$ 上。求证：$AB = AC$。
（2）如图 2 所示，点 $O$ 在 $\triangle ABC$ 的内部。求证：$AB = AC$。

答案： 9.证明:
(1)在Rt△OEC和Rt△OFB中，
∵$\begin{cases} OE = OF, \\ OC = OB, \end{cases}$
∴Rt△OEC≌Rt△OFB(HL),
∴∠B=∠C,
∴AB=AC;
(2)在Rt△OEC和Rt△OFB中，
∵$\begin{cases} OE = OF, \\ OC = OB, \end{cases}$
∴Rt△OEC≌Rt△OFB(HL),
∴∠OBF=∠OCE.
　又
∵OB=OC,
∴∠OBC=∠OCB,
∴∠FBO+∠OBC=∠OCE+∠OCB，
　即∠ABC=∠ACB,
∴AB=AC.

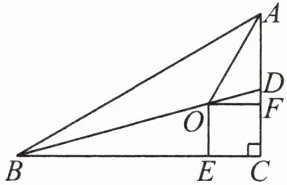
10. 如图，在 $Rt\triangle ABC$ 中，$\angle C = 90^{\circ}$，$BD$ 是 $Rt\triangle ABC$ 的一条角平分线，点 $O$，$E$，$F$ 分别在 $BD$，$BC$，$AC$ 上，且四边形 $OECF$ 是正方形。
（1）求证：点 $O$ 在 $\angle BAC$ 的平分线上。
（2）若 $AC = 5$，$BC = 12$，求 $OE$ 的长。

答案：
10.
(1)证明:过点O作OM⊥AB于点M，
∵正方形OECF，
∴OE=EC=CF=OF,
　OE⊥BC于E,OF⊥AC于F,
∵BD平分∠ABC,OM⊥AB于M,
∴OM=OE=OF,
∴点O在∠BAC的平分线上;
　　　　　　　　　
(2)解:
∵Rt△ABC中,∠C=90°,AC=5,
　BC=12,
∴AB=13,
∴BE=BM,AM=AF,
　又
∵BE=BC−CE,AF=AC−CF,
　而CE=CF=OE,
∴BE=12−OE,
　AF=5−OE,
∴BM+AM=AB,
　即BE+AF=13,12−OE+5−OE=13,
∴OE=2.