《2025年名师面对面学科素养评价八年级数学上册浙教版》

6. 如图，在 $ \triangle ABC $ 和 $ \triangle ADE $ 中，$ \angle BAC = \angle DAE = 90^{\circ} $，$ AB = AC $，$ AD = AE $，$ C $，$ D $，$ E $ 三点在同一条直线上，连结 $ BD $。
(1) 求证：$ \triangle BAD \cong \triangle CAE $。
(2) 试猜想 $ BD $，$ CE $ 有何特殊的位置关系，并证明。

答案： 6.
(1)证明：
∵∠BAC=∠DAE=90°，
∴∠BAC+∠CAD=∠DAE+∠CAD，
即∠BAD=∠CAE.
又
∵AB=AC,AD=AE，
∴△BAD≌△CAE(SAS).
(2)解：BD⊥CE.证明如下：
由
(1)知△BAD≌△CAE，
∴∠ADB=∠E.
∵∠DAE=90°,
∴∠E+∠ADE=90°，
∴∠ADB+∠ADE=90°，
即∠BDE=90°,
∴BD⊥CE.

7. 如图，在 $ \triangle ABC $ 和 $ \triangle AED $ 中，$ AB = AC $，$ AE = AD $，$ \angle BAC = \angle EAD $，且点 $ E $，$ A $，$ B $ 在同一条直线上，点 $ C $，$ D $ 在直线 $ EB $ 同侧，连结 $ BD $，$ CE $ 相交于点 $ M $。
(1) 求证：$ \triangle ABD \cong \triangle ACE $。
(2) 若 $ \angle CAD = 100^{\circ} $，求 $ \angle DME $ 的度数。

答案： 7.
(1)证明：
∵∠BAC=∠EAD，
∴∠DAB=∠EAC.
又
∵AB=AC,AD=AE，
∴△ABD≌△ACE(SAS).
(2)解：
∵∠CAD=100°，
∴∠CAB=∠DAE=40°，
∴∠DME=∠CEB+∠DBE=∠CEB+∠ECA=∠CAB
=40°.

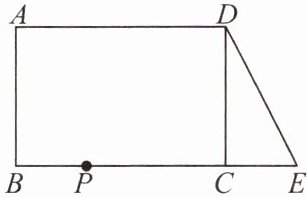
8. 【空间观念、推理能力】如图，在长方形 $ ABCD $ 中，$ AB = 4 $，$ AD = 6 $，延长 $ BC $ 到点 $ E $，使 $ CE = 2 $，连结 $ DE $。动点 $ P $ 从点 $ B $ 出发，以每秒 $ 2 $ 个单位长度的速度沿 $ BC \to CD \to DA $ 向终点 $ A $ 运动。设点 $ P $ 的运动时间为 $ t $ s，当 $ t $ 为何值时，$ \triangle ABP $ 和 $ \triangle DCE $ 全等？

答案： 8.解：
∵AB=CD,∠A=∠B=∠DCE=90°，
∴△ABP≌△DCE或△BAP≌△DCE.
当△ABP≌△DCE时，BP=CE=2，
此时2t=2，解得t=1；
当△BAP≌△DCE时，AP=CE=2，
此时BC+CD+DP=BC+CD+(DA-AP)=6+4+(6-
2)=14，即2t=14，解得t=7.
∴当t=1s或7s时，△ABP和△DCE全等.