《2025年名师面对面学科素养评价八年级数学上册浙教版》

3. 如图，在四边形$ABCD$中，$AD// BC$，$E$为$CD$的中点，连结$AE$，$BE$，延长$AE$交$BC$的延长线于点$F$。
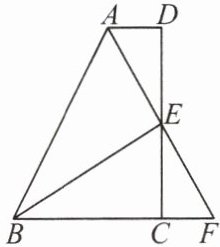
(1) 求证：$\triangle DAE\cong\triangle CFE$。
(2) 若$BE\perp AF$，求证：$AB = BC + AD$。

答案： 3.证明：
(1)
∵ AD // BC，
∴ ∠ADC = ∠ECF.
∵ E 是 CD 的中点，
∴ DE = EC.
∵ ∠AED = ∠FEC，
∴ △ADE≌△FCE(ASA)；
(2)由
(1)知△ADE≌△FCE，
∴ AE = EF，AD = CF.
∵ BE ⊥ AE，
∴ ∠BEA = ∠BEF = 90°.
∵ BE = BE，
∴ △ABE≌△FBE(SAS)，
∴ AB = BF = BC + CF = BC + AD.

4. (1) 如图 1，已知$AB = 8$，$AC = 6$，点$D$是$BC$的中点，则中线$AD$的取值范围是1＜AD＜7。
(2) 如图 2，在$\triangle ABC$中，点$D$是$BC$的中点，点$E$是边$AB$上的一点，作$DF\perp DE$交边$AC$于点$F$，连结$EF$。试判断$BE + CF$与$EF$的大小关系，并证明你的结论。

答案：
4.解：
(1)如图 1，延长 AD 到 E，使 AD = DE，连结 BE，易证：△ADC≌△EDB，
∴ 1＜AD＜7；
　　
(2)如图 2，延长 ED 到 G，使 ED = DG，连结 CG，FG，易证：△BDE≌△CDG，
∴ BE = CG.
∵ ED = DG，∠EDF = ∠GDF，DF = DF，
∴ △FDE≌△FDG，
∴ EF = GF.
在△FGC 中，FC + CG ＞ FG，
∴ BE + CF ＞ EF.