6. 有一条直的等宽纸带,按如图所示的方式折叠,则∠α的度数等于(
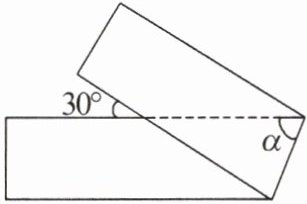
A.50°
B.60°
C.75°
D.85°
C
)
A.50°
B.60°
C.75°
D.85°
答案:
6.C
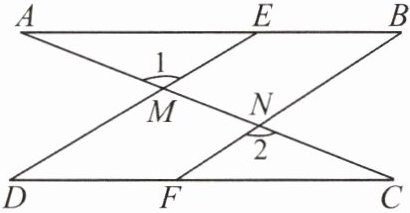
7. 如图,有三个论断:①∠1 = ∠2;②∠B = ∠D;③∠A = ∠C. 请从中任选两个作为条件,另一个作为结论构成一个命题,并证明该命题的正确性.

答案:
7.解:已知:∠B=∠D,∠A=∠C.
求证:∠1=∠2.
证明:
∵∠A=∠C,
∴AB//CD,
∴∠B=∠BFC.
∵∠B=∠D,
∴∠BFC=∠D,
∴DE//BF,
∴∠DMN=∠BNM.
∵∠1=∠DMN,∠2=∠BNM,
∴∠1=∠2.
(此题答案不唯一)
求证:∠1=∠2.
证明:
∵∠A=∠C,
∴AB//CD,
∴∠B=∠BFC.
∵∠B=∠D,
∴∠BFC=∠D,
∴DE//BF,
∴∠DMN=∠BNM.
∵∠1=∠DMN,∠2=∠BNM,
∴∠1=∠2.
(此题答案不唯一)
8. 实验证明,平面镜反射光线的规律如下:射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等.
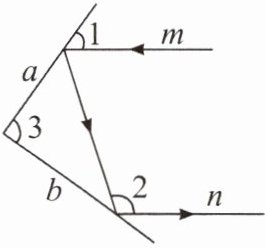
(1) 如图,一束光线m射到平面镜上,被平面镜a反射到平面镜b上,又被平面镜b反射. 若被平面镜b反射出的光线n与光线m平行,且∠1 = 50°,则∠2 =
(2) 在(1)中,若∠1 = 55°,则∠3 =
(3) 猜想:当两平面镜a,b的夹角∠3 =
(1) 如图,一束光线m射到平面镜上,被平面镜a反射到平面镜b上,又被平面镜b反射. 若被平面镜b反射出的光线n与光线m平行,且∠1 = 50°,则∠2 =
100°
,∠3 =90°
.(2) 在(1)中,若∠1 = 55°,则∠3 =
90°
;若∠1 = 40°,则∠3 =90°
.(3) 猜想:当两平面镜a,b的夹角∠3 =
90°
时,可以使任何射到平面镜a上的光线m,经过平面镜a,b的两次反射后,入射光线m与反射光线n平行,请说明理由.
答案:
8.
(1)100° 90°
(2)90° 90°
(3)90°
如图.
∵∠3=90°,
∴∠4+∠5=90°.
又
∵∠1=∠4,∠5=∠6,
∴∠2+∠7=180°−(∠5+∠6)+180°−(∠1+∠4)
=360°−2∠4−2∠5
=360°−2(∠4+∠5)
=180°,
∴m//n.

8.
(1)100° 90°
(2)90° 90°
(3)90°
如图.
∵∠3=90°,
∴∠4+∠5=90°.
又
∵∠1=∠4,∠5=∠6,
∴∠2+∠7=180°−(∠5+∠6)+180°−(∠1+∠4)
=360°−2∠4−2∠5
=360°−2(∠4+∠5)
=180°,
∴m//n.

查看更多完整答案,请扫码查看


